Determine o módulo do campo magnético de um fio retilíneo de comprimento , por onde passa uma corrente , num ponto situado a uma distância do fio. Dê a resposta em função dos ângulos e formados entre a normal ao fio baixada do ponto e pelas retas que unem o ponto com as extremidades do fio considerado.
Passo 1
A figura abaixo representa a configuração dada no enunciado.
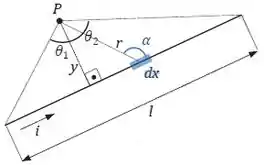
Vamos utilizar a lei de Biot-Savart para encontrar o campo magnético . Temos que:
já que o ângulo entre os vetores e é igual a .
Passo 2
Precisamos, agora encontrar uma relação de com o ângulo , já que os dois estão variando com . Para isso, vamos olhar para o triângulo retângulo abaixo:
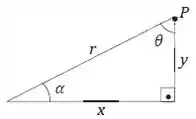
Da figura, a gente pode concluir que
E também que
Agora, precisamos relacionar o ângulo com o raio . Temos que:
Passo 3
Vamos substituir todas as relações encontradas no Passo 2 na expressão de :
Passo 4
Agora, já podemos integrar a expressão do Passo 3 para encontrar o módulo do campo magnético . Mas antes vamos checar os limites de integração. Se a gente olhar para as duas figuras, vemos que o ângulo varia, na verdade, de até . Serão esses, então, os nossos limites. Vamos lá: