O circuito da figura é formado por dois arcos de círculo de raios e e dois fios retilíneos de comprimento . Cada arco forma um setor de ângulo igual a . O circuito é percorrido por uma corrente de intensidade no sentido indicado. Calcule, justificando:
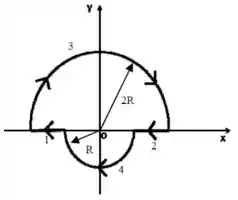
As contribuições e dos segmentos retilíneos, e
As contribuições e dos arcos de raio e
para o campo magnético (módulo, direção e sentido) na origem dos eixos , que corresponde ao centro dos dois arcos de círculo.
Considere agora que o arco de raio gire de em torno do eixo (= eixo de rotação).
Calcule os novos campos magnéticos e
Enfim, o circuito da figura acima é girado de um ângulo , conforme indica a Figura abaixo:
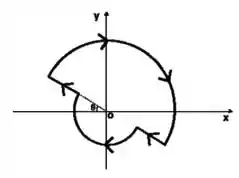
Calcule os novos campos magnéticos e .
Passo 1
As contribuições e dos segmentos retilíneos.
Pra facilitar a nossa vida aqui, vamos usar a Lei de Biot-Savart, ela nos diz que:
Temos que tomar cuidado com o sentido dos campos magnéticos para saber se eles se somam, ou não, no final dos cálculos.
Na dúvida, vamos adotar o seguinte referencial.
Passo 2
Para os segmentos retilíneos 1 e 2, vamos começar dando uma olhada na direção do produto vetorial.
É importante lembrar que o vetor unitário aponta sempre na direção do ponto onde queremos calcular o campo magnético (no caso, o ponto ). E o vetor aponta sempre no sentido da corrente.
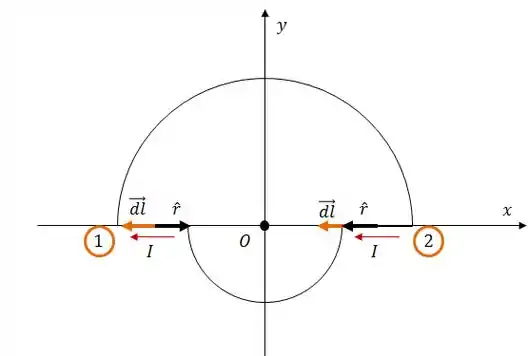
Como você pode ver, os dois vetores e ou são paralelos, ou são antiparalelos... de qualquer forma, o produto vetorial entre os dois vai ser nulo... ou seja:
Assim:
Passo 3
As contribuições e dos arcos de raio e
Arco maior
Novamente, vamos começar dando uma olhada na direção do produto vetorial.
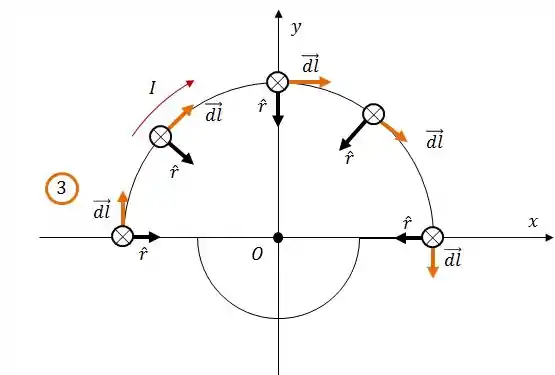
Se você calcular com calma, pode ver que o ângulo é sempre :
Substituindo, tiramos fora da integral:
Além disso, temos que nesse caso o é constante:
Enquanto a integral de é o comprimento do arco, ou seja, o comprimento de meio círculo de raio
Passo 4
Arco menor
O raciocínio é absolutamente o mesmo.
Calculando a direção do produto vetorial:
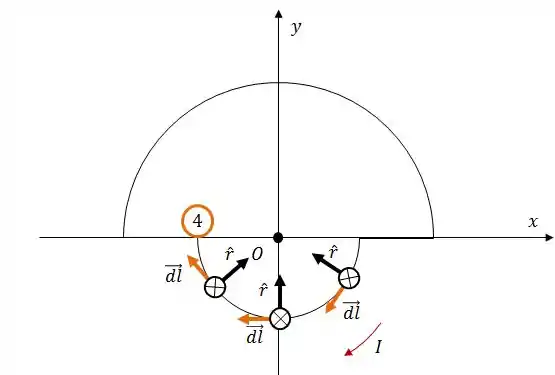
Se você calcular com calma, pode ver que o ângulo é sempre :
Daí, seguindo o mesmo caminho do Passo 3, só que agora para o arco de raio , vamos encontrar o seguinte:
Passo 5
Calcule os novos campos magnéticos e
Bom, o que aconteceu aqui é que agora o circuito vai ter essa cara aqui:
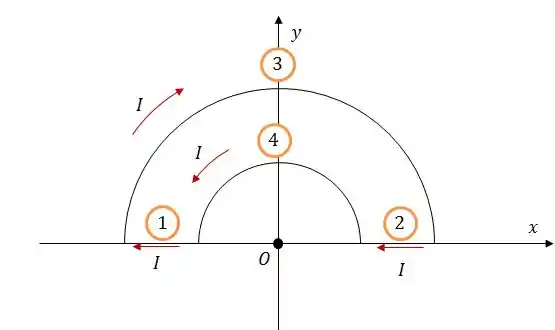
Beleza, nos fios 1, 2 e 3 não vai mudar nada em relação aos vetores e . Logo:
Em relação ao arco 4, o que muda é a direção do campo magnético gerado por ele... dá uma olhada:
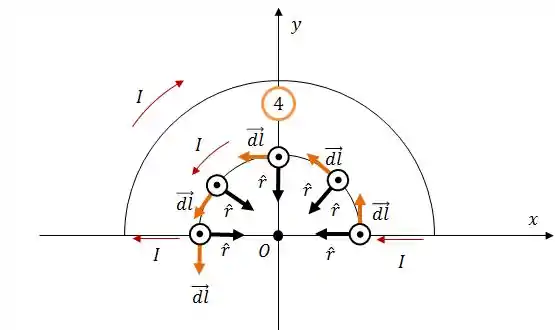
A diferença aqui então é que o campo magnético aponta agora no sentido . Como a geometria do problema permanece a mesma, o módulo de permanece o mesmo.
Passo 6
Calcule os novos campos magnéticos e .
Como aqui só estamos rotacionando em torno do ponto , os vetores de campo magnéticos permanecem os mesmos do primeiro caso. Já que a geometria do problema é a mesma e os vetores vão continuar apontando nos mesmos sentidos.
Logo:
Resposta