A figura abaixo é composta por um fio, perpendicular ao plano da página, por onde passa uma corrente e por uma espira, no plano da página, com dois arcos de circunferência de raio e compreendidos entre um ângulo de .
Pela espira passa uma corrente de e o centro da mesma coincide com o fio no ponto .
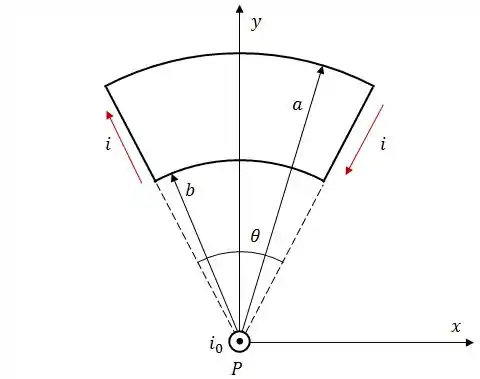
Determine:
O vetor momento de dipolo magnético da espira;
O vetor campo magnético no ponto ;
O torque que o campo do fio produz sobre a espira;
Passo 1
O vetor momento de dipolo magnético da espira;
Por definição, o momento de dipolo magnético é dado por:
Onde a direção e sentido do momento de dipolo magnético são determinados pelo sentido da corrente através da regra da mão direita. Nesse caso, com a corrente flui no sentido horário, o momento de dipolo magnético terá direção perpendicular ao plano da página, apontando para dentro da página, no sentido .
A única coisa que temos que fazer agora é calcular a área da espira.
Passo 2
Você consegue ver que a espira é como se fosse uma fatia de uma coroa circular?
Uma coroa circular completa tem área igual a:
Assim, podemos calcular área da espira com uma regra de 3 simples:
Onde e
Por fim, o momento de dipolo magnético é dado por:
Passo 3
O vetor campo magnético no ponto ;
O campo magnético total no ponto será igual a
Como o ponto coincide com o fio de corrente , o campo magnético gerado por no ponto será nulo.
O campo gerado pela espira é calculado através da Lei de Biot-Savart. Entretanto, a primeira coisa que temos que fazer aqui é dividir a espira em 4 partes.
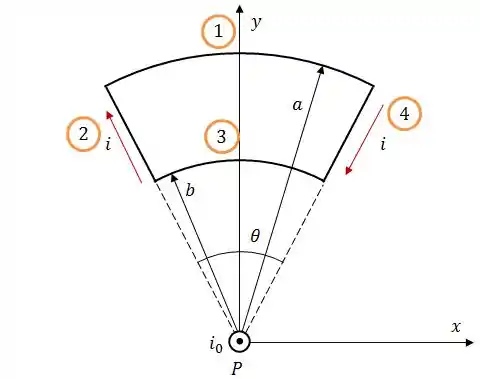
A Lei de Biot Savart é dada por:
Vamos analisar cada fio separadamente.
Passo 4
- Fios 2 e 4
- Fio 1
- Fio 3
Vamos começar por eles porque eles tem uma particularidade. Vamos analisar os vetores e .
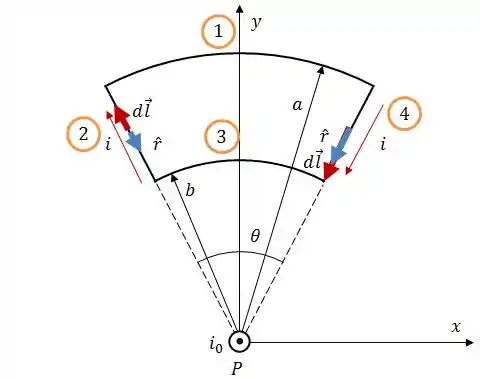
Em ambos os casos, e são paralelos ou antiparalelos, isso significa que:
Logo:
No fio 1, os vetores e possuem os seguintes sentidos:
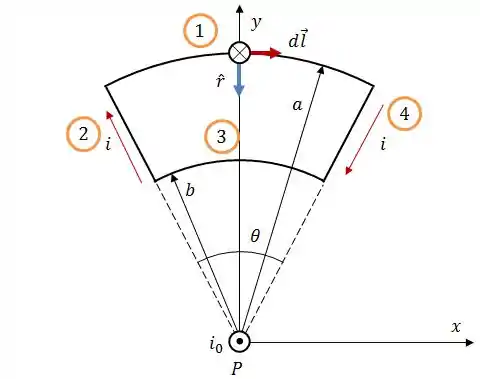
Assim, voltando à Lei de Biot Savart, teremos :
Onde , e .
No fio 3, os vetores e possuem os seguintes sentidos:
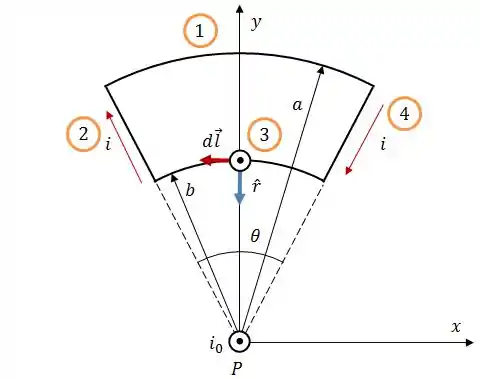
No final das contas, o trabalho é muito parecido com o que tivemos no Fio 1. As únicas diferenças são que agora o campo magnético aponta na direção e , logo:
Portanto, o campo magnético resultante será:
Substituindo os valores:
Passo 5
O torque que o campo do fio produz sobre a espira;
O torque magnético sobre uma espira é dado por:
O campo magnético gerado por sobre a espira é dado por:
O problema aqui é que o raio varia, logo, o campo magnético também varia. Assim, para achar o torque total, vamos fazer o seguinte... visto que e são sempre perpendiculares:
Onde .
Pra sabermos em que sentido estará o torque, na dúvida, basta verificar para onde estarão as forças sobre os fios 2 e 4.
Pela regra da mão direita, no fio 2, apontará no sentido e, no fio 4, apontará no sentido . Como resultado, a espira terá uma rotação no sentido . Logo:
Como o problema não nos forneceu o valor de , só podemos escrever o torque resultante como:
Resposta