Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Biot-Savart Geral

Ver Teoria
Exercício 531234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515254555657585960616263646566676869707172737475767778

Enunciado

Considere o circuito da figura abaixo, composto por dois lados retilíneos e dois arcos de círculo, ambos definidos por um ângulo θ .

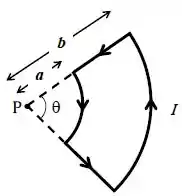
O menor arco está a uma distância a do ponto P e o maior a uma distância b do mesmo ponto P . O circuito é percorrido por uma corrente I no sentido anti-horário.

Assinale a opção que especifica corretamente o vetor campo magnético resultante em P .

a μ 0 I θ   ( b - a ) / ( 2 π a b ) , perpendicular ao plano da página e entrando na página.

b μ 0 I θ   ( b - a ) / ( 4 π a b ) , perpendicular ao plano da página e entrando na página.

c μ 0 I θ   ( a + b ) / ( 2 π a b ) , perpendicular ao plano da página e entrando na página.

d μ 0 I θ   ( a + b ) / ( 4 π a b ) , perpendicular ao plano da página e saindo da página.

e μ 0 I θ   ( b - a ) / ( 2 a b ) , perpendicular ao plano da página e saindo da página.

Passo 1

O campo magnético formado por arcos podem ser calculados a partir da Lei de Biot-Savart:

B → = μ 0 4 π I ∫ fio   d l → × r ^ r 2

  • Arco maior:

    • No caso desse arco, o produto vetorial será dado por:

    d l → × r ^ = d l z ^

    Substituindo, tiramos - z ^ fora da integral:

    B → = μ 0 4 π I z ^ ∫ fio   d l r 2

    Além disso, temos que nesse caso o r é constante:

    r = b

    B → = μ 0 4 π b 2 I z ^ ∫ fio   d l

    Enquanto a integral de d l é o comprimento do fio:

    B → = μ 0 4 π b 2 I z ^ θ b

    B → = μ 0 I θ 4 π b z ^

    Passo 2

  • Arco menor:

No caso desse arco, o produto vetorial será dado por:

d l → × r ^ = d l - z ^

Substituindo, tiramos - z ^ fora da integral:

B → = - μ 0 4 π I z ^ ∫ fio   d l r 2

Além disso, temos que nesse caso o r é constante:

r = a

B → = - μ 0 4 π a 2 I z ^ ∫ fio   d l

Enquanto a integral de d l é o comprimento do fio:

B → = - μ 0 4 π a 2 I z ^ θ a

B → = - μ 0 I θ 4 π a z ^

Passo 2

Nos casos dos fios retilíneos, d l → e r ^ são paralelos, logo:

d l → × r ^ = 0

B → = 0

Passo 3

Assim, o campo magnético resultante será:

B → = μ 0 I θ 4 π b z ^ - μ 0 I θ 4 π a z ^

B → = μ 0 I θ 4 π 1 b - 1 a z ^

B → = - μ 0 I θ b - a 4 π a b z ^  

Entrando na página.

Resposta

b μ 0 I θ   ( b - a ) / ( 4 π a b ) , perpendicular ao plano da página e entrando na página.

Exercícios de Livros Relacionados

14- Uma partícula com carga 6.40 × 10 - 19C se desloca ao longo de uma órbita circular com raio igual a 4.68m m , em virtude da força oriunda de um campo magnético de módulo 1.65T , cuja direção é per
15- Um elétron no ponto A da Figura 27.46 possui velocidade v 0 igual a 1.41 × 10 6m / s . Determine: ( a ) o módulo, a direção e o sentido do campo magnético que obriga o elétron a descrever uma órbi
16- Repita o Exercício 27.15 para o caso no qual a partícula é um próton em vez de um elétron.
Dois fios longos estão no plano x y e conduzem correntes no sentido positivo do eixo x . O fio 1 está em y = 10,0c m e conduz uma corrente de 6,00A ; o fio 2 está em y = 5,00c m e conduz uma corrente
Na figura 29-63, cinco fios paralelos longos no plano x y estão separados por uma distância d = 8,00c m , têm 10,0m de comprimento e conduzem correntes iguais de 3,00A para fora do papel. Em termos do