i. Considere uma espira quadrada de lado percorrida no sentido anti-horário por uma corrente . A espira se encontra no plano , conforme a figura.
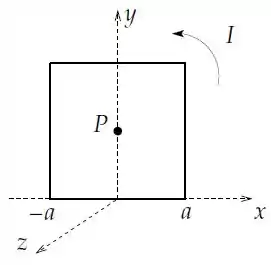
(a) Calcule o vetor campo magnético produzido pelo segmento da espira ao longo do eixo no centro da espira (ponto ).
(b) Calcule o vetor campo magnético total produzido pelos quatro segmentos no centro da espira.
Passo 1
(a) Calcule o vetor campo magnético produzido pelo segmento da espira ao longo do eixo no centro da espira (ponto ).
Vamos ter que usar a lei de Bio-Savart pra salvar a nossa vida aqui.
Ah! Podemos escreve essa fórmula da seguinte forma (PS: não quis fazer essa rima escrota):
Primeiro vamos começar determinando quem é , e .
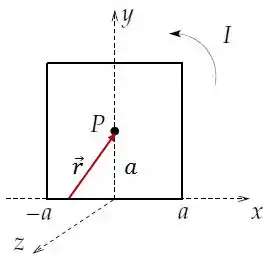
O vetor deve seguir o sentido da corrente, logo, .
Olhando a figura:
Assim:
Voltando para fórmula:
Parece uma integral escrota? Deve ser porque é uma integral escrota...
Mas relaxa, no formulário tem a resposta dessa integral:
Passo 2
(b) Calcule o vetor campo magnético total produzido pelos quatro segmentos no centro da espira.
Aqui não tem muito mistério... se os 4 fios são iguais, os 4 fios vão produzir campo magnéticos iguais, logo:
Resposta
i. Campo magnético no centro da espira quadrada:
(a)
(b)