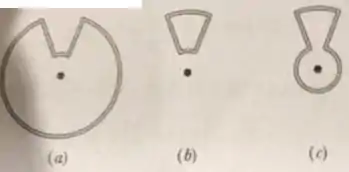
A figura mostra três circuitos formados por dois segmentos radiais e dois arcos de circunferência concêntricos, um de raio e outro de raio . A corrente é a mesma nos três circuitos e o ângulos entre os dois segmentos radiais é o mesmo. Colocando os circuitos na ordem do módulo decrescente do campo magnético no centro dos arcos (marcado na figura por um ponto), obtemos
a) .
b) .
c) .
d) .
e) nenhuma das respostas está correta.
Passo 1
Fala pessoal, bora fazer mais uma questão sobre campo magnético?
Para resolver esse problema temos que saber qual é campo magnético produzido por um arco circular no centro da espira. A expressão é a seguinte:
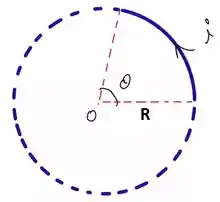
Nessa expressão, é o ângulo em radianos e o campo para fora da tela (regra da mão direita). Note que se tivermos o círculo fechado (), achamos a conhecida fórmula da espira circular:
Para deduzir essa fórmula temos que usar a lei de Biot-Savart e isso é feito nossos resumos, dá uma olhadinha lá!
Passo 2
Vamos olhar para a figura (a). Nela, temos uma espira com arco e raio e outra com raio e arco . Assim, o campo total será
É importante ressaltar que os fios na direção radial não contribuem com o campo no centro da espira pois a linha de ação deles passa pelo centro da espira. Além disso, note que eu somei os campos pois o sentido da corrente é o mesmo nos dois, de modo que podemos somá-los.
Já na figura (b), o sentido da corrente em arco circular é diferente. Com isso, temos que subtrair uma contribuição pela outra. Note também que agora os dois arcos têm o mesmo ângulo :
Comparando a situação (a) com a (b), vemos que na primeira aparece um fator extra somando, de modo que
Passo 3
Vamos olhar agora para a figura (c). A primeira coisa que notamos é que as duas correntes estão no mesmo sentido e os campos vão se somar! Agora temos um raio por um ângulo e um raio por um ângulo , de modo que
Será que conseguimos achar uma relação que vale para qualquer , e ?
Vamos chutar por exemplo e . Daí,
Vemos que de fato . No passo 2 provamos que isso é verdade sempre. Mas olha com carinho para . Para pequeno tipo , temos que
Portanto, nesse caso, . Todavia, se escolhemos um ângulo maior, tipo :
Logo, nesse caso . Com isso vemos que dependendo da escolha do ângulo a ordem de quem é maior que quem pode mudar. A única garantia que temos sempre é .
Desta forma, não temos muita escolha senão marcar alternativa E...
Resposta
Alternativa E.