Um anel circular, de raio , situado no plano , com centro na origem, transporta uma corrente elétrica estacionária de intensidade e sentido indicado, como mostrado no lado esquerdo (a) da figura abaixo.
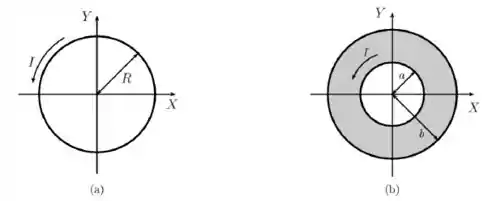
- Utilizando a lei de Biot-Savart, determine o campo magnético (módulo, direção e sentido) produzido pelo anel na origem
Considere, agora, uma coroa circular condutora, de raios interno e externo , também situada no plano e com centro na origem, transportando uma corrente elétrica estacionária de intensidade , uniformemente distribuída através de sua superfície, como mostrado no lado direito (b) da mesma figura.
b) Determine o campo magnético (módulo, direção e sentido) produzido pela coroa na origem. Sugestão: imagine a coroa como vários anéis concêntricos de raio e largura infinitesimal , através dos quais passa uma corrente de intensidade
Passo 1
a) Considere um elemento de comprimento infinitesimal do anel, orientado no sentido da corrente, como mostrado na figura abaixo. Esse elemento é sempre tangente ao anel em todos os seus pontos.
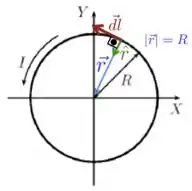
Pela lei de Biot-Savart, sua contribuição para o campo magnético em um ponto qualquer do espaço é dada por:
onde é a distância do elemento ao ponto e é o unitário da direção que aponta do elemento para o ponto. Pela figura, podemos ver que, na origem, para todos os pontos do anel e que
pois o ângulo entre esses dois vetores vale . Assim,
Para obter o campo total, basta integrar sobre o anel. Obtemos, então:
que vai resultar em
Passo 2
b) Vamos seguir a sugestão do enunciado e vamos dividir a coroa em anéis infinitesimais de raio variável e espessura infinitesimal . A corrente que passa por cada um desses anéis é dada por:
uma vez que a corrente está uniformemente distribuída sobre a área da coroa. Pelo resultado do item anterior, a contribuição de um anel infinitesimal como este para o campo magnético no centro da coroa é dada por:
O campo total pode ser obtido integrando sobre os anéis que compõem a coroa. Assim:
que resulta em