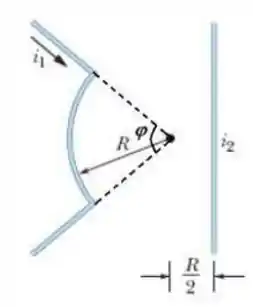
A figura abaixo mostra dois fios. O fio é formado por um arco de circunferência de raio e dois segmentos radiais que conduz uma corrente no sentido indicado. O fio é muito longo e retilíneo, conduz uma corrente que pode ser ajustada e está a uma distância do centro do arco. O campo magnético produzido pelas duas correntes é medido no centro de curvatura do arco. Determine o ângulo , em graus, subtendido pelo arco e o sentido da corrente para que o valor do campo magnético no centro do arco seja nulo. Use a Lei de Biot-Savart para o fio e a Lei de Ampére para o fio .
Passo 1
Fala aí galera, tudo bom com vocês?
Nessa questão temos um probleminha envolvendo campo magnético gerado por corrente elétrica em um fio. Basicamente, temos um fio em formato de arco circular (fio ) e um fio reto muito longo (fio , que consideraremos infinito.
Esses fios geram um campo elétrico em um ponto entre eles, mostrado na imagem. A grande questão é que não sabemos qual o ângulo do arco do fio .
O nosso objetivo é determinar esse ângulo sabendo que o campo no ponto indicado deve ser nulo.

Então, pra fazer isso precisamos conhecer as expressões que regem o campo magnético gerado por cada um desses fios. Como o próprio enunciado já nos falou, para o fio devemos usar a Lei de Biot-Savart que diz:
onde é a constante de permeabilidade magnética no vácuo, é a corrente que passa pelo fio, é o comprimento do fio e é a distância de cada elemento do fio até o ponto que queremos calcular o campo.
Já para o fio vamos usar a Lei de Ampére que diz que:
Nesse caso, traçamos uma curva “imaginária” de comprimento . é o campo magnético em cada ponto dessa curva, é a corrente que cruza a superfície delimitada por essa curva.
Massa! Agora que revisamos essas fórmulas, vamos colocar a mão na massa!
Iremos primeiro descobrir a expressão do campo para ambos os fios, e depois usamos o fato de que o campo resultante é nulo no ponto indicado no enunciado.
Passo 2
Bom, vamos começar calculando o campo magnético gerado pelo fio . Trata-se de um fio infinito, como a fórmula do campo gerado por esse fio é bastante utilizada, vale a pena decorá-la.
Mas, usando a ideia da lei de Ampére, pela simetria do fio dizemos que todos os pontos a uma distância do fio estão sujeitos a um mesmo campo magnético.
Assim, temos:
Pois o campo magnético é constante e por ir pra fora da integral. E, a circunferência em volta do fio tem comprimento (que equivale à soma dos elementos ). Logo:
No caso do nosso fio , temos e a distância para o ponto considerado vale . Assim:
E, pela regra da mão direita, temos que esse campo aponta para fora do plano dos fios.
Muito bom!
Passo 3
Vamos analisar agora o fio . Ele é composto por partes: duas partes são de fios retos e uma parte é de um arco circular.
O mais interessante aqui, é que pela lei de Biot-Savart o campo magnético é dado pela expressão:
Assim, ele depende do produto vetorial do vetor elemento do fio e do vetor distância de cada elemento de fio ao ponto considerado. Maaaaas, no caso das duas partes retas do fio , o vetor elemento do fio, e o vetor distância, , são paralelos. E, o produto de dois vetores paralelos é sempre nulo.
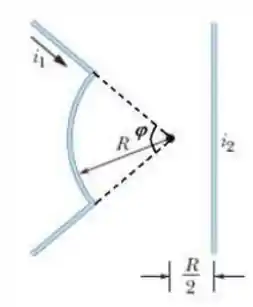
Assim, na prática, a única parte do fio que irá provocar campo magnético no ponto considerado é o arco circular!! Legal né?
Vamos então usar Biot-Savart para calcular esse campo.
Como o ponto considerado está no centro do arco circular de raio , temos que para cada elemento do fio. Além disso, o produto vetorial:
Aponta sempre para dentro do plano dos fios, que convencionaremos como o sentido negativo para o campo. Assim, temos:
Quando somamos os elementos do fio em um arco, temos o comprimento desse arco, que vale:
Assim, finalmente chegamos a expressão para o campo magnético provocado pelo fio :
Como , temos:
Excelente!
Passo 4
Pra finalizar, vamos usar a informação de que o campo magnético resultante no ponto considerado é nulo. Ou seja:
Daí, considerando que aponta no sentido negativo e no sentido positivo, temos:
Logo, isolando , chegamos que:
Prontinho gente! Descobrimos que o ângulo do arco para do fio para que o campo magnético seja nulo no ponto considerado vale .
É isso galera, obrigado pela atenção! Até a próxima 😊