Considere um fio infinito formado por dois trechos retilíneos semi-infinitos e perpendiculares entre si, ligados por um arco de circunferência de raio R (um quarto de circunferência). Por esse fio flui uma corrente estacionária , como mostrado na Figura . Utilize o sistema de eixos cartesianos desenhado na Figura . Com essa escolha, um dos trechos retilı́neos é paralelo ao eixo , enquanto o outro é paralelo ao eixo , e o arco de circunferência tem centro na origem .
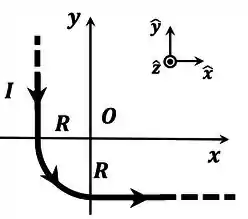
(a) Determine a contribuição ao campo magnético na origem do sistema de coordenadas indicado na Figura , devido ao trecho do fio correspondente ao arco de circunferência. Indique o módulo, a direção e o sentido de .
(b) Determine a contribuição ao campo magnético na origem do sistema de coordenadas indicado na Figura , devido ao trecho horizontal do fio. Indique o módulo, direção e sentido de .
(c) Determine o campo magnético (módulo, direção e sentido) produzido pelo fio completo, na origem do sistema de coordenadas.
Passo 1
Para calcular o campo gerado pelo arco de circunferência precisamos usar a lei de Biot-Savart
Nesse caso demos que a distância de um elemento de comprimento até a origem é constante e igual ao raio do arco, .
O vetor é o vetor unitário apontando do elemento do arco até a origem (onde queremos calcular o campo) e o vetor é tangente ao arco indo na direção da corrente, conforme a figura
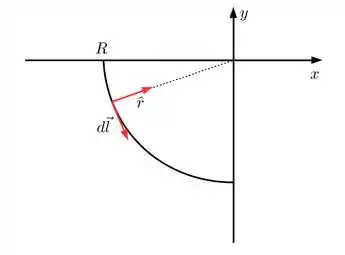
Como os vetores e são perpendiculares entre si e os dois estão contidos no plano o seu produto vetorial será na direção . Pela regra da mão direita, sabemos que o campo magnético tem que apontar na direção positiva do eixo .
*Uma justificativa mais matemática é que e , então ;)
Só que esse elemento é o elemento de arco de um círculo de raio , então
Assim o nosso campo magnético é dado por
Passo 2
Agora vamos calcular o campo gerado por um fio semi-infinito. Para isso usaremos de novo Biot-Savart.
Dessa vez o nosso elemento de fio está localizado em . A distância desse ponto até a origem é
E o vetor unitário é dado por
E o vetor , eu defini no sentido da corrente
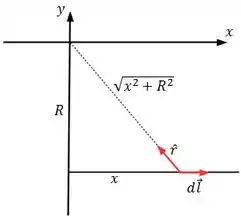
Assim o produto vetorial fica
E a lei de Biot-Savart fica
Possivelmente, tem no seu formulário que
Assim a nossa integral fica
Assim
Passo 3
Agora temos simplesmente que o campo total gerado pelo fio é dado por
Já que os dois fios semi-infinitos gerarão o mesmo campo.
Resposta
Ei, a resposta está no passo a passo :)