Considere a figura a seguir, em que um arco de meia circunferência de raio porta uma corrente no sentido horário e a origem do sistema de coordenadas coincide com o centro do arco.
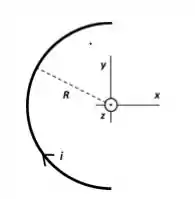
(a) Usando explicitamente a lei de Biot-Savart, calcule o vetor campo magnético (módulo, direção e sentido) produzido pelo arco na origem.
Sabemos que um fio retilíneo infinito que transporta uma corrente produz um campo magnético, a uma distância do fio, cujo módulo é dado por .
(b) Considere que o campo produzido na origem pelo arco da figura seja dado por .
Deseja-se posicionar um fio retilíneo infinito paralelo ao eixo de modo a anular o campo resultante na origem. Se o fio retilíneo porta uma corrente de no sentido , calcule a coordenada (incluindo o sinal) onde o fio deve ser posicionado.
(c) Partindo agora de uma situação em que o campo resultante é nulo na origem, encontre os dois únicos modos de posicionar um novo fio retilíneo de maneira a que o novo campo resultante possua somente componente . (Ou seja, encontre ao longo de qual direção e sentido deve estar a corrente do fio, e em que região do espaço ele deve ser posicionado).
Passo 1
(a)
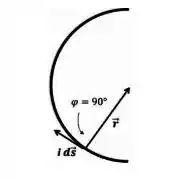
A Lei de Biot-Savart é dada por:
Colocando as constantes pra fora da integral, e fazendo o produto vetorial:
Fazendo a substituição e colocando o intervalo de integração para :
Como é constante:
Logo:
Passo 2
(b) Queremos que: . Assim, em módulo:
Substituindo os valores:
E então:
Como o fio porta corrente no sentido e queremos que seu campo possua sentido , o fio deve ser posicionado ao longo coordenada .
Passo 3
(c) Na verdade há não apenas dois modos, mas infinitos modos de conseguirmos um campo no sentido na origem: o fio retilíneo pode ser colocado em qualquer orientação no plano , contanto que não passe pela própria origem e contanto também que o sentido de sua corrente seja compatível com a regra da mão direita. Listamos as quatro possibilidades mais visualizáveis:
MODO 1: fio cortando o eixo em pontos tais que e com corrente no sentido ;
MODO 2: fio cortando o eixo em pontos tais que e com corrente no sentido ;
MODO 3: fio cortando o eixo em pontos tais que e com corrente no sentido ;
MODO 4: fio cortando o eixo em pontos tais que e com corrente no sentido .
Resposta
a)
b)
c) 4 modos visualizáveis:
MODO 1: fio cortando o eixo em pontos tais que e com corrente no sentido ;
MODO 2: fio cortando o eixo em pontos tais que e com corrente no sentido ;
MODO 3: fio cortando o eixo em pontos tais que e com corrente no sentido ;
MODO 4: fio cortando o eixo em pontos tais que e com corrente no sentido .