a) Um fio de comprimento infinito e raio desprezível transporta uma corrente . Utilize a lei de Biot-Savart e calcule o campo magnético a uma distância do fio.
b) Um fio, de raio desprezível, e que transporta uma corrente é configurado na forma de uma espira circular de raio . Utilize a lei de Biot-Savart e calcule o campo magnético no centro da espira.
Passo 1
Fala galerinha, beleza?
Nesse problema vamos usar a lei de Biot-Savart para deduzir o campo de um fio infinito e de uma espira circular. O legal é que já sabemos os resultados que devemos encontrar. Para o fio infinito,
Já para a espira circular de raio , no centro, o campo será
Se você quiser ver essas deduções com todo detalhe do mundo, aconselho você dar uma espiada nos resumos do RespondeAí, aqui vou fazer de forma mais resumida senão a resolução fica muito grande...
Passo 2
Para o fio infinito, vamos considerar primeiro um fio de comprimento e calcular o campo a uma distância do seu centro:
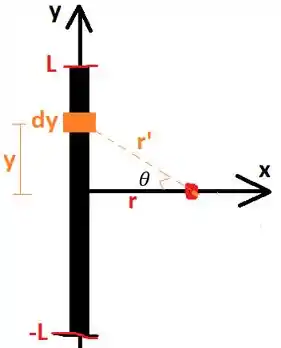
A lei de Biot-Savart estabelece que o campo de um pedacinho do fio em uma posição é dado por
Nessa expressão, é a distância do elemento de corrente até a posição onde vamos calcular o campo.
Olhe com atenção para a figura: note que o eixo aponta para fora da tela! Considere o elemento de comprimento do fio posicionado a uma distância da origem. Isso significa que a corrente está subindo no fio, de baixo para cima. Vamos calcular o campo devido a essa contribuição.
Observe que
Além disso, o vetor pode ser decomposto em
Com isso, o produto vetorial da
Isso significa que
Note que esse campo aponta para dentro da tela e isso vai acontecer para qualquer porção do fio que escolhermos, incluindo a parte de baixo do fio. Portanto, vemos que o campo resultante apontará para dentro da tela (o que concorda com a regra da mão direita que conhecemos).
Passo 3
Note também que
Assim,
Substituindo a expressão de :
Daí, para achar o campo total, basta integrar de até :
Essa integral pode ser calculada com uma substituição
Logo,
Precisamos escrever o em função de e :
Assim,
Portanto,
Fazendo as contas:
Como estamos olhando apenas para o módulo:
Para o fio infinito, tomamos o limite :
Assim, para o fio infinito, o campo é
Essa é a boa e velha expressão que conhecemos!
Passo 4
Agora vamos tentar calcular o campo da espira circular.
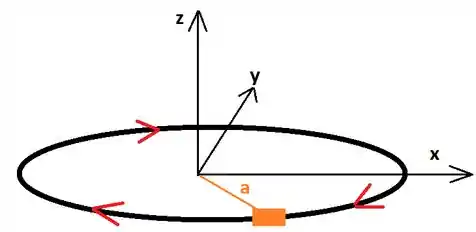
Vamos considerar a porção do fio de comprimento pintada em laranja. O produto vetorial vai apontar na direção :
Lembre-se que nesse caso, . Assim,
Integrando sobre o círculo todo:
Olhando apenas para o módulo e vendo que o resultado da integral é , achamos
Esse resultado bate com o esperado! Assim, fechamos o problema 😉.