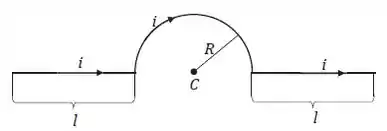
O fio que aparece na figura abaixo é percorrido por uma corrente . Qual é o valor da contribuição para o campo magnético no centro da semicircunferência devido
(a) a cada segmento retilíneo de comprimento ;
(b) à semicircunferência de raio ; e
(c) a todo fio?
Passo 1
(a) Contribuição dos segmentos retilíneos de comprimento .
Aqui, vamos aplicar a lei de Biot-Savart, que é dada por:
Bem, vamos começar olhando para a figura abaixo:
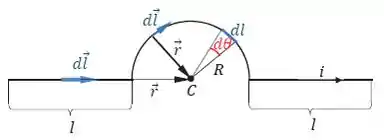
Daí a gente já consegue concluir que, tanto para o segmento retilíneo da esquerada, como para o da direita, temos que:
já que esses vetores são paralelos entre si. Isso significa que esses segmentos não contribuem para o campo magnético em .
Passo 2
(b) Contribuição da semicircunferência de raio .
Já para a semicircunferência, podemos concluir da figura que:
Substituindo na expressão de , temos:
Integrando:
Se usarmos a regra da mão direita para determinar direção e sentido do campo, vemos que ele é perpendicular ao plano da folha e aponta para dentro dela.
Passo 3
(c) Contribuição de todo o fio.
A contribuição total é a soma de todas as contribuições. Mas como o campo em gerado pelos dois segmentos de reta é nulo, o campo magnético total em vai ser aquele calculado no item (b), dado por:
Resposta
(a)
(b)
(c)