Considere o circuito da figura, por onde circula uma corrente . Os segmentos curvos são arcos de círculos com raios e e ângulo . Os segmentos retos estão dispostos ao longo dos raios.
- Use a lei de Biot-Savart para encontrar a expressão literal para o campo magnético no ponto . Substitua os valores e indique o valor do módulo do campo.
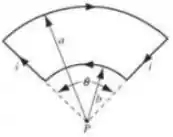
Passo 1
Oi, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! Vamos lá?
Vamos começar pela lei de Biot-Savart:
Nossa missão aqui é separar esse circuito em quatro segmentos e calcular a contribuição de cada um deles. O campo resultante vai ser a soma dos campos, beleza?

Então vamos começar!
Passo 2
Vamos começar analisando os segmentos retos, aqueles que estão dispostos ao longo dos raios.
Pela lei de Biot-Savart o diferencial de campo é
Como o circuito é composto por 4 segmentos, o não é o mesmo. Assim, o produto vetorial
É o que mais queremos saber! Aquele é o vetor diferencial de caminho ao longo da trajetória que estamos analisando. Vou destacar em rosa os caminhos para você identificar melhor
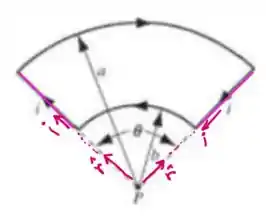
Sendo assim, não temos contribuição desses segmentos para o campo magnético em P!
Tudo bem até aqui?
Passo 3
Agora vamos analisar o arco menor, vou destacar ele em roxo e já aplicar a regra da mão direita para determinar o sentido do campo magnético
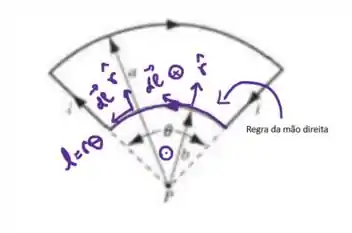
Em P esse segmento contribui com uma componente positiva, para fora da página. E o produto vetorial é entre o vetor diferencial de caminho, tangente ao pedacinho de fio e perpendicular ao vetor unitário ,
E o resultado é um vetor para fora de comprimento . O comprimento é o comprimento de arco, e integrando o diferencial campo magnético
Temos na integral. E o comprimento de arco quando tem uma abertura angular e uma distância do eixo de referência é , com .
Sendo assim o campo magnético devido a esse segmento é
Tranquilo?

Passo 4
Agora precisamos calcular a contribuição para o campo magnético devido ao outro arco. O procedimento é bem similar!
Vou destacar no desenho e aplicar a regra da mão direita para determinar o sentido do campo no ponto P:
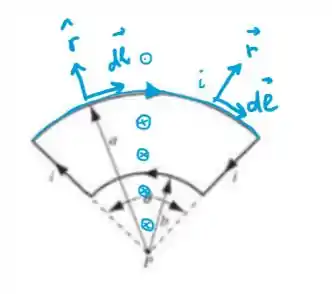
Tranquilo?
Passo 5
E por fim, o campo total no ponto P é a soma das contribuições dos segmentos dos fios:
E o módulo do vetor é:
Beleza?
Passo 6
O último passo é substituir os valores de e para calcular o campo:
 show! Vamos para a próxima?
show! Vamos para a próxima?