Mostre que o módulo do campo magnético produzido no centro de uma espira retangular de comprimento e largura , percorrida por uma corrente é dado por:
Passo 1
A espira tem mais ou menos essa cara aqui:
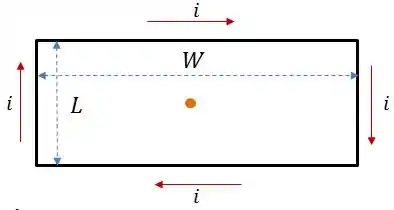
Pra resolver a nossa vida aqui, vamos usar a Lei de Biot-Savart, que nos diz que:
Vamos fazer o seguinte então... vamos calcular um campo magnético para o fio vertical e um campo magnético para o fio horizontal. Feito isso, é só multiplicarmos por dois.
Passo 2
Vou começar pelo fio vertical de comprimento . Vamos adotar a seguinte orientação:
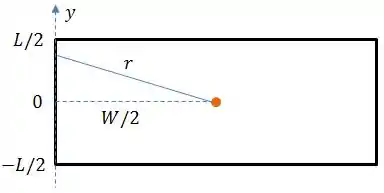
Dessa forma:
Agora precisamos resolver a parte do :
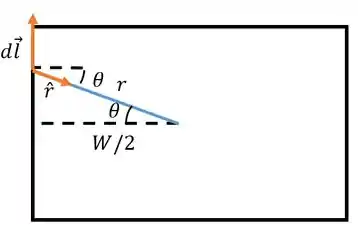
Vamos quebrar um pouco a cabeça aqui...
Ah! Como chamamos a direção vertical de , ao invés de usar , vou usar .
Geometricamente falando:
Ou seja:
Agora sim... montando a integral da Lei de Biot-Savart:
O módulo do campo vai ser então
Ajeitando isso aqui...
Passo 3
Então, agora nós faríamos para o fio horizontal... mas concorda que o raciocínio seria o mesmo? Trocando apenas o pelo ...
Seguindo o pensamento, para o fio horizontal:
Passo 4
Como se tratam de dois fios verticais e dois horizontais, o campo magnético resultante é dado por:
Vamos colocar o que der em M.M.C. pra tentar organizar essa bagaça...
Por último...
ACABOU!
Resposta
Ei, a resposta está no passo a passo :)