Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Ampère

Ver Teoria
Exercício 140123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Considere correntes elétricas de mesma intensidade, entrando ou saindo da página da prova, conforme os circuitos abaixo.

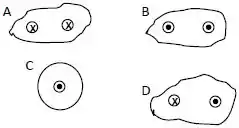
Circuito A : Duas correntes entrando

Circuito B : Duas correntes saindo

Circuito C : Uma corrente saindo

Circuito D : Uma corrente entrando e outra saindo

Integrando no sentido anti-horário, classifique a integral de linha do campo magnético, ou seja, ∮ B → . d l → , começando do maior positivo.

a A = B > C > D

b A > C > B > D

c D > B > C > A

d A > D > B > C

e B > C > D > A

Passo 1

Essa integral corresponde à Lei de Ampère, dada por:

∮ C   B → ∙ d l → = μ 0 I i n t

Assim, como estamos integrando no sentido anti-horário, utilizando a regra da mão direita, as corrente que estiverem saindo da página serão positivas, e as correntes que estiverem entrando na página serão negativas.

Dessa forma, as integrais nas curvas A , B , C e D serão:

∮ A   B → ∙ d l → = - 2 μ 0 I

∮ B   B → ∙ d l → = + 2 μ 0 I

∮ C   B → ∙ d l → = + μ 0 I

∮ D   B → ∙ d l → = 0

Logo, organizando na ordem decrescente, teremos:

B > C > D > A

Resposta

e B > C > D > A

Exercícios de Livros Relacionados

41- Um supercondutor do tipo I I em um campo magnético externo entre B c 1 e B c 2 possui regiões supercondutores e regiões com resistência na qual existe campo magnético. Qual é a resistência de um c
A figura 29-86 mostra uma seção reta de um condutor cilíndrico oco de raios a e b que conduz uma corrente i uniformemente distribuída. (a) Mostre que, no intervalo bra , o módulo B ( r ) do campo elét
74- Um condutor possui forma de um cilindro oco, sendo a o raio interno e b o raio externo. Ele conduz uma corrente I uniformemente distribuída ao longo da sua seção reta. Deduza expressões para o mód
81- Um plano infinito que conduz uma corrente. Condutores retilíneos longos, com seções retas quadradas, cada um deles conduzindo uma corrente I , são colocados um ao lado do outro, formando uma placa
82- Condutores retilíneos longos, com seções retas quadradas, cada um deles conduzindo uma corrente I , são colocados um ao lado do outro, formando uma placa fina que se estende até o infinito, sendo