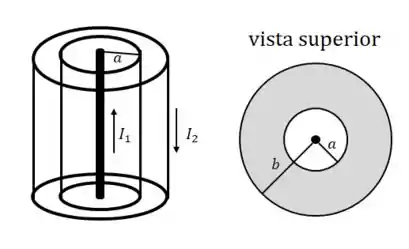
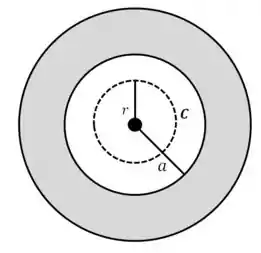
Considere um fio condutor envolvido por uma camada cilíndrica condutora coaxial ao fio, de raio interno e raio externo (a região logo ao redor do fio, até a distância , é vácuo). O fio é percorrido pr uma corrente , e a camada é percorrida por uma corrente uniformemente distribuída, na mesma direção de , mas com sentido oposto. Considere o fio e a camada como sendo muito longos.
a) Calcule a densidade de corrente na camada cilíndrica.
Calcule o módulo do campo magnético a uma distância do fio (eixo da camada), tal que:
b) .
c) .
d) .
Passo 1
Então pessoal, vamos começar lembrando o que é densidade de corrente. A definição matemática mais útil é essa aqui:
O que essa integral diz? Que a densidade de corrente é a grandeza que, quando é integrado ao longo de uma superfície, te dá a corrente total que passa por ali.
Então beleza, no nosso caso a gente quer calcular a densidade de corrente na camada cilíndrica: aquela região pintada de cinza no desenho.
A corrente que passa por aquela camada é :
O vetor densidade de corrente tem a mesma direção da corrente. No nosso caso essa região é paralela à altura do cilindro.
E o elemento de área é perpendicular à seção reta do cilindro, ou seja, paralelo à densidade de corrente.
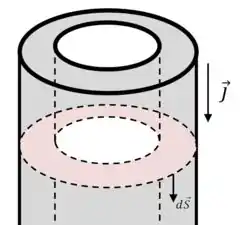
Como os dois vetores são paralelos e apontam no mesmo sentido (a gente pode escolher o sentido do vetor ), aquele produto interno fica assim:
Passo 2
Vamos colocar isso na nossa integral:
E a densidade de corrente é constante ao longo de toda a superfície (que é aquele anel pintado de vermelho no desenho). Então podemos tirar da integral:
Agora essa integral virou simplesmente a área da superfície :
Só o que a gente fez aí foi usar a fórmula para área do círculo. Sabendo que o círculo de fora tem área e o círculo de dentro tem área .
Agora é só isolar :
Passo 3
Beleza, qual é o próximo passo? O enunciado quer que a gente calcule o campo magnético produzido pela corrente no fio.
Vamos começar entendendo do que ele está falando.
Quando um fio é percorrido por uma corrente, surge um campo magnético em torno dele. A direção dele segue essa regra aqui:
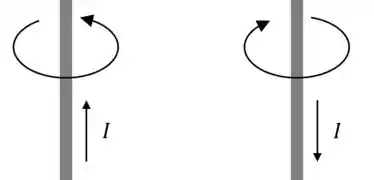
Pra lembrar disso é só apontar seu polegar direito na direção da corrente: a direção em que seus outros dedos se curvam para fechar a mão é a “direção” do campo.
Atenção, isso é só uma forma de lembrar, o vetor campo magnético na verdade é tangente a essa trajetória em cada ponto:
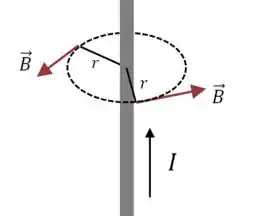
A equação que dá a intensidade desse campo é a lei de Ampére:
Vamos ver como se usa essa equação na prática.
Passo 4
(b) Primeiro queremos calcular o campo magnético quando . Lembrando que aqui é a distância radial até o centro do fio.
Então tá, o primeiro passo pra usar a lei de Ampére é escolher uma curva para a nossa integral.
Como a gente quer considerar a região , vamos escolher uma circunferência que tem um raio nesse intervalo. Olhando de cima, vamos ficar com algo assim:
Então vamos voltar para a integral:
A corrente no fio está apontando para cima, então (como a gente mostrou no passo anterior) a direção do campo vai ficar assim:
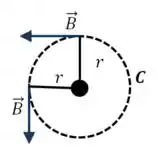
Se a nossa integral percorrer a curva no sentido anti-horário, então o elemento de comprimento vai sempre ter a mesma direção e sentido do campo:
Substituindo na integral:
O campo é o mesmo em todos os pontos da curva, então:
Agora essa integral do lado esquerdo é simplesmente o comprimento da circunferência :
O é a corrente total que atravessa a circunferência. Nesse caso, essa é a corrente que passa no fio, então:
E o vetor campo magnético é simplesmente esse módulo apontando na direção tangente à circunferência que a gente construiu. Vamos chamar essa direção de ( de “normal” à trajetória), então:
Obs.: O enunciado pediu só o módulo do campo, mas precisamos da forma vetorial pra poder usar no próximo item.
Passo 5
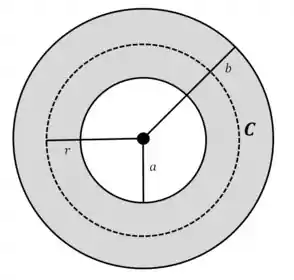
(c) Agora a gente quer fazer a mesma coisa, mas para uma região maior:
Ou seja, agora estamos procurando o campo na região dentro da camada cilíndrica.
Bom, o campo gerado pelo fio continua o mesmo, então isso aqui continua valendo:
Mas tem mais campo nessa história! O campo gerado pela corrente que passa na camada cilíndrica: vamos pensar só nele agora.
Tá, todo aquele raciocínio de antes continua valendo: vamos escolher uma curva na região que foi pedida:
O que vai mudar agora em relação à conta que a gente fez antes?
Primeiro: a corrente que atravessa a camada está apontada para baixo! Então o campo produzido por ela está no sentido horário, e a gente optou por percorrer a curva no sentido anti-horário, então:
Ou seja:
Ok, agora vem a segunda diferença: qual é a corrente total que atravessa a nossa curva ?
Passo 6
Bom, a gente já considerou a corrente que passa pelo fio, então vamos olhar só a corrente que vem da camada mesmo.
Lá no item (a) nós calculamos a densidade de corrente na camada:
Se você multiplicar essa densidade de corrente pela área da camada que está contida na nossa curva , vamos ter a corrente total que atravessa a curva!
Olhando pelo desenho ali de cima, dá pra ver que a área da camada (parte cinza), dentro da curva é:
Então:
Substituindo com a fórmula da densidade :
Substituindo na fórmula lá de cima:
Assim como fizemos antes, a versão “vetorial” desse campo é:
Agora é só juntar com o campo produzido pelo fio para achar o campo total nessa região:
Simplificando um pouco:
E o módulo do campo magnético nessa região (como foi pedido) é:
Pronto!
Passo 7
(c) Beleza, agora só falta calcular o campo do lado de fora do conjunto todo:
Vamos dar mais uma olhada na equação que a gente escreveu para a região :
Quando a gente estiver bem na borda da região, onde , olha o que acontece com o campo:
E conforme o raio aumenta ainda mais, a quantidade de corrente envolvida naquela nossa curva não vai mudar!
Ou seja, o campo é:
E tem módulo:
Resposta
(a) A densidade de corrente é .
(b) O módulo do campo na região é .
(c) O módulo do campo na região é .
(d) O módulo do campo na região é .