Lei de Ampère, Forças e Torque sobre uma Espira
Dois fios 1 e 2, infinitos e paralelos, separados pela distância , conduzem no vácuo, cada um, uma corrente , em sentidos opostos, conforme a figura.
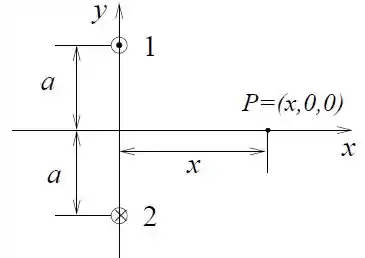
- Usando a lei de Ampère, calcule o vetor campo magnético produzido por um fio infinito por onde passa uma corrente a uma distância do fio.
- Calcule o vetor campo magnético produzido pelos dois fios no ponto .
- Calcule o vetor força por unidade de comprimento exercida no fio 2 pelo fio 1.
Passo 1
- Usando a lei de Ampère, calcule o vetor campo magnético produzido por um fio infinito por onde passa uma corrente a uma distância do fio.
- Calcule o vetor campo magnético produzido pelos dois fios no ponto .
- Calcule o vetor força por unidade de comprimento exercida no fio 2 pelo fio 1.
Beleza, a lei de Ampère vai nos ajudar a calcular o módulo do campo magnético... assim que calcularmos o módulo, nós falamos sobre o vetor:
A nossa curva é uma circunferência de raio , logo:
Show! Se olharmos o fio “de cima” com a corrente saindo da tela, vamos ver que o campo magnético tem o seguinte sentido:
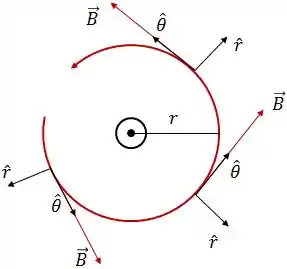
Então vai facilitar a nossa vida se usarmos coordenadas polares pra essa representação do vetor campo magnético em qualquer ponto.
Passo 2
O vetor campo magnético produzido pelos dois fios vai ser a resultante da soma a vetorial dos campos magnéticos produzidos por cada fio.
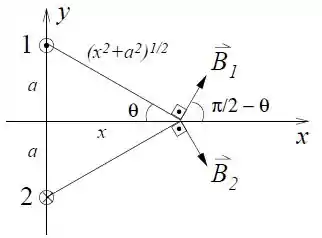
Como a distância entre cada fio e o ponto é a mesma e como o módulo da corrente também é a mesma.
Olhando a figura, dá pra perceber logo de cara que as componentes em vão se anular e as componentes em vão se somar. Logo:
Ah! Lembrando que .
Voltando pra figura, podemos ver que:
Substituindo na equação de :
Passo 3
A força exercida no fio 2 pelo fio 1 é dada por:
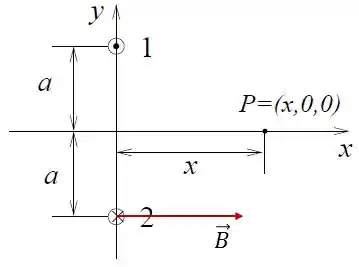
Pela regra da mão direita, vemos que .
E como a corrente do fio 2 está entrando no papel, . Logo: