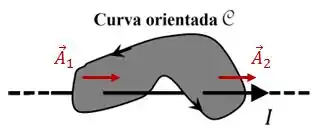
A figura abaixo mostra uma curva fechada, orientada, e um trecho de um fio retilíneo, longo, pelo qual passa uma corrente estacionária de intensidade , no sentido indicado.

Podemos afirmar que:
;
;
;
;
;
Passo 1
A lei de Ampère é dada por:
Onde é a soma das correntes que passam pela curva. Neste caso, a mesma corrente atravessa a curva duas vezes, então devemos levar essas duas passagens em consideração.
Para determinar se vamos considerar a corrente positiva ou negativa, devemos utilizar a orientação do vetor área. Onde a mesma é dada de acordo com a orientação da curva.
Para isso, vamos utilizar a regra da mão direita, onde os quatro dedos da sua mão (tirando o polegar) estarão na mesma orientação da curva, e o polegar indicará a orientação do vetor área.
Passo 2
Se a corrente tiver o mesmo sentido do vetor área, deve ser considerada positiva, caso contrário, negativa.
Aqui, nos dois casos a corrente possui o mesmo sentido do vetor área, logo:
Finalmente:
Resposta
;