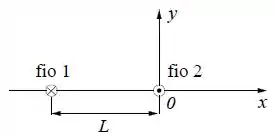
A figura abaixo mostra uma seção transversal de dois fios condutores longos (fio 1 e fio 2) estendidos paralelamente um ao outro, ao longo da direção . Por estes fios circulam correntes e , em sentidos opostos, sendo no mesmo sentido do eixo , conforme a figura.
Usando a Lei de Ampère calcule o vetor campo magnético de um fio infinito por onde passa uma corrente .
Calcule o vetor campo magnético total devido aos dois fios mostrados na figura para um ponto qualquer do eixo com .
Passo 1
Usando a Lei de Ampère calcule o vetor campo magnético de um fio infinito por onde passa uma corrente .
A Lei de Ampère é dada por:
Como se trata de um fio retilíneo e infinito, a amperiana será uma circunferência de raio . Assim, como é uniforme ao longo da amperiana:
O resultado da integral será o comprimento da circunferência. Assim:
Como o campo magnético tem sempre a direção e sentido tangencial à circunferência, podemos escrever o vetor campo magnético como:
Passo 2
Calcule o vetor campo magnético total devido aos dois fios mostrados na figura para um ponto qualquer do eixo com .
Usando a regra da mão direita, sobre o eixo todos os campo magnéticos estarão na direção do eixo .
O campo magnético gerado pelo fio 1, para qualquer ponto sobre o eixo onde , estará sempre no sentido e . Logo:
O campo magnético gerado pelo fio 2, para qualquer ponto sobre o eixo onde , estará sempre no sentido e . Logo:
Assim, o campo magnético total devido aos dois fios será:
Resposta