UFF – Física 2 – Provas Antigas – P3 – 2022.1 – Questão 10
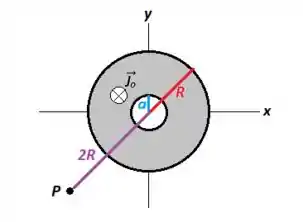
A figura mostra a seção transversal de um cilindro condutor longo de raio , percorrido por uma corrente de densidade uniforme de módulo apontando para dentro da página. Nele existe uma cavidade oca também cilíndrica, de raio 𝑎 = 4 𝑐𝑚, centrada com o eixo do cilindro. Sabendo que o cilindro se encontra sobre o eixo , calcule o módulo do vetor campo magnético em um ponto que está a uma distância do centro do cilindro.
(a)
(b)
(c)
(d)
(e)
Passo 1
Eaee!!! Belezinha? Olha.. basicamente nessa questão queremos descobrir o vetor do campo magnético em um ponto a partir de uma corrente que passa por um cilindro condutor!
Aí eu te pergunto: Como podemos encontrar esse vetor do campo magnético tendo a densidade de corrente que percorre o cilindro?
Pois bem, vamos ter que relembrar a equação da Lei de Ampère:
Passo 2
Bom... como no ponto sabe-se que que o campo é perpendicular à circunferência de raio igual a , temos para a integral:
Já para a corrente, sabendo que sua densidade é de , e sabendo que ela percorre a área do cilindro grande menos a área da parte oca, temos:
Passo 3
Assim, substituindo as duas equações, temos:
Entendeu direitinho? Responde aee ;)
Resposta
(e)