Um fio condutor na figura abaixo conduz uma corrente no sentido indicado. Para e os trechos são retilíneos e estão ao longo de e , respectivamente (fios semi- infinitos). Para e menores do que , o condutor forma um quarto de círculo com raio , conforme a figura 1.
Quais são os campos no ponto devido aos segmentos retilíneos do fio?
Qual é o campo no ponto devido ao segmento circular?
Determine o valor da integral de linha do vetor ao longo do percurso circular fechado não coplanar com os fios e centrado no eixo , conforme a figura 2.
Passo 1
Quais são os campos no ponto devido aos segmentos retilíneos do fio?
Pra determinar o campo formado pelos segmentos retilíneos, vamos ter que recorrer à Lei de Biot-Savart, dada por:
Onde é um pedaço infinitesimal do segmento, cujo vetor aponta sempre na direção e sentido da corrente e é o vetor unitário que vai do elemento ao ponto onde queremos calcular o campo magnético.
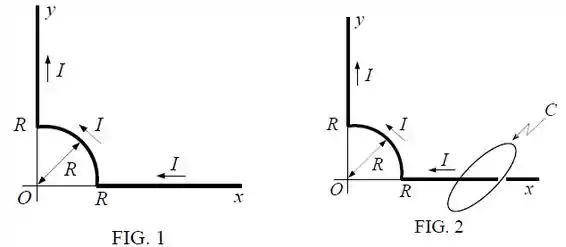
Pra começar, vamos dar uma olhada em e em cada segmento:
Daqui podemos ver que os vetores e são paralelos (segmento horizontal) ou são anti-paralelos (segmento vertical).
Em ambos os casos:
Logo:
Passo 2
Qual é o campo no ponto devido ao segmento circular?
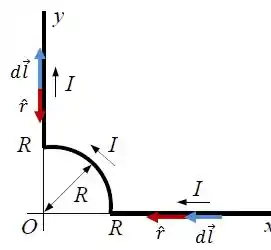
Agora, vamos observar os vetores e no segmento circular:
Daqui, podemos observar que o vetor vai estar sempre tangente ao segmento circular, enquanto vai estar sempre apontando pro centro do segmento circular.
Usando a regra da mão direita, podemos dizer que
Logo, substituindo na Lei de Biot-Savart:
Onde e são constantes. Logo:
Essa integral vai calcular exatamente o tamanho do segmento circular, assim:
Passo 3
Determine o valor da integral de linha do vetor ao longo do percurso circular fechado não coplanar com os fios e centrado no eixo , conforme a figura 2.
A “integral de linha do vetor ao longo do percurso fechado circular ” é a definição da Lei de Ampère, que é dada por:
Onde é a corrente que atravessa a curva . Nesse caso, , logo:
Resposta