Um fio condutor fino, retilíneo e infinito carrega uma corrente estacionária de intensidade , como mostrado na figura abaixo. Considere uma curva imaginária fechada e orientada na forma de um círculo de raio , desenhada de forma que seu plano seja perpendicular ao eixo do fio, mas seu centro não coincida com ele, como indicado.

b) Neste item, é interessante que a gente revise algumas propriedades gerais do campo   gerado pela corrente e dado pela lei de Biot-Savart, cuja expressão é

em que   é o elemento de comprimento ao longo do fio pelo qual passa a corrente e   , sendo que o versor (vetor unitário) está na direção raio  e, por isso, define a direção chamada de radial.

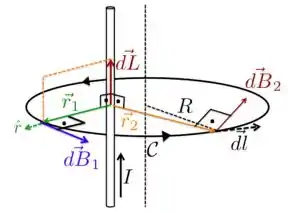
Para revisar as propriedades gerais, acompanhe os itens abaixo sempre considerando a figura acima e a equação acima para te ajudar a fixar os conceitos:

1. A direção e sentido do campo magnético são dados pelo produto vetorial  ;
2. O campo magnético é perpendicular tanto à   quanto à e, portanto, perpendicular ao plano gerado pelo produto vetorial  , conforme ilustra o retângulo em laranja pontilhado na posição onde está   na figura acima. Essas conclusões também valem para o campo   (dá uma conferida nisso para firmar as ideias!!);
3. O campo magnético não pode ter componente na direção do fio, pois é sempre perpendicular ao elemento   pelo qual passa;

Essas propriedades são gerais e independem de o fio estar no centro da curva fechada ou não. IMPORTANTE!

Mas então o que muda no caso do fio que a questão comenta? Continua que conto...

No caso do fio fora do centro da curva , o vetores   não necessariamente são paralelos aos elementos tangentes à curva fechada . Tome, por exemplo, o caso do campo  . Ele é perpendicular a   (elemento do fio) e também a  , mas não está na direção do vetor tangente  , como mostrado na figura.

c) Para respondermos este item da questão com propriedade, “bora” fazer uma resumo do que a gente já sabe:

1. o campo magnético gerado pelo fio que está fora do centro de não é o mesmo em todos os pontos de , porque depende da distância ao fio do cilindro e essa distância é diferente para diferentes pontos de .
2. o campo magnético gerado pelo fio que está fora do centro de , apesar de SEMPRE ser perpendicular a   e a  , não é tangente a todos os pontos de .

Uma forma de obter o campo magnético produzido por uma corrente é utilizar a lei de Ampère

sendo que a corrente é a corrente total que atravessa a área delimitada pela curva fechada .

Como discutimos, o campo magnético depende apenas da distância ao fio, mas que, como o fio não está no centro da curva, esse campo não é o mesmo em todos os pontos de . Por isso, não podemos tirar o módulo de dentro da integral acima!

Além disso, como o ângulo entre e   varia ao longo de , produto escalar   também varia. Por isso, não é possível calcular o campo nesse caso.

CUIDADO, MAS MUITO CUIDADO MEEEESMOOO: não significa que a lei de Ampère não vale no caso do fio da questão! Significa apenas que, nas condições do problema, não é possível obter o campo magnético a partir da lei de Ampère! Isso é MUITO IMPORTANTE e você deve LEVAR PARA A VIDA essa informação...rsrs

Sugestão: tente reproduzir, passo a passo, os argumentos teóricos dessa questão, pois são fundamentais. Note que a gente não precisou fazer nenhuma integral, derivada, ou produto vetorial complicado para tirar conclusões importantes sobre as leis de Biot-Savart e de Ampère!! Provavelmente, você utilizará o que aprendeu aqui para resolver outras questões...