Um fio espesso é constituído por um cilindro condutor infinito de seção transversal circular de raio . Nesse cilindro, passa uma densidade de corrente uniforme e estacionária dada por , onde é o unitário da direção paralela ao eixo do cilindro. Nessa situação, o que se pode dizer a respeito do campo magnético produzido por esse fio?
- O campo magnético é nulo em qualquer ponto sobre o eixo do fio
- O campo magnético é paralelo ao eixo do fio em qualquer ponto no interior do mesmo
- O campo magnético é uniforme no interior no fio
- O campo magnético é perpendicular ao eixo do fio e aponta radialmente para fora em qualquer ponto no exterior do mesmo
- O módulo do campo magnético cai com o inverso do quadrado da distância ao eixo do fio no exterior do mesmo
Passo 1
Primeiro, vamos discutir como é o campo magnético produzido por uma corrente estacionária e um ponto qualquer gerado por esse fio infinito. Para isso, vamos analisar suas principais características utilizando a lei de Biot-Savart
em que é a corrente que está no sentido de . Os elementos dessa expressão estão representados na figura abaixo. Note, primeiramente, que o campo magnético depende do produto vetorial e que é esse produto vetorial que dá o sentido e direção do campo magnético.
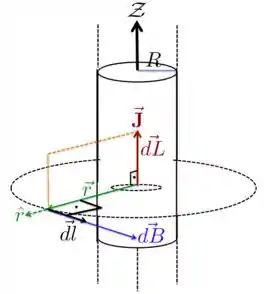
Portanto, como mostra a figura, o campo é perpendicular tanto à , quanto à . Ou seja, o campo magnético é perpendicular ao plano formado pelos vetores e , o que mostramos na figura como o plano delimitado pela linhas tracejadas na cor laranja.
Por isso, o campo magnético é tangencial à circunferência e não tem componente radial, ou seja, na direção de . Resumo:
- é perpendicular a e a e, portanto, perpendicular ao plano formado por esses dois vetores;
- é tangencial ao círculo e, por isso, não tem nenhuma componente na direção de ;
Com essas observações a partir da lei de Biot-Savart, já conseguimos eliminar os itens (b) e (d) da questão, que estão INCORRETOS.
Sugestão: reveja essas características, pois elas são gerais e tendem a serem cobradas com frequência.
Passo 2
Bom, agora, o segundo passo é saber como é o módulo de , já que apenas analisamos sua direção e o sentido.
Para ver como fica o módulo, utilizaremos a lei de Ampère para os círculos tracejados da figura, um para e o outro para .
Região :
Como a densidade de corrente é uniforme dentro do cilindro (), a corrente que passa na área é dada por
Beleza? O campo magnético não pode ter nenhuma componente na direção de (veja o Passo 1 acima!) e é sempre paralelo ao elemento tangente à curva fechada tracejada (não confunda este elemento com aquele ! CUIDADO! Dá uma olhada na figura para ver que são diferentes).
Além disso, o campo tem o mesmo valor para todos os pontos em cima da circunferência e, por isso, podemos escrever que
Portanto, o campo magnético varia linearmente com a distância perpendicular ao fio. Isso nos mostra que o campo dentro do fio não é uniforme. Isso nos permite também concluir que para (isto é, exatamente em cima do eixo do cilindro), temos
O item c, por essa razão, está INCORRETO, enquanto o item a está CORRETO.
Passo 3
Região :
Nessa região, a corrente no interior da área delimitada pelo círculo tracejado da figura é
uma vez que toda a corrente está atravessando a área delimitada pelo círculo em questão. Isso nos dá, pela lei de Ampère, que
que varia com o inverso da distância ao eixo do fio no seu exterior.
Isso torna o item e) INCORRETO.
Resposta
Portanto, a resposta correta é a letra a) .