UFMG – Fundamentos de Eletromagnetismo – P2 – Questão 3a
Uma fita metálica de largura conduz uma corrente . Portanto, a densidade superficial de corrente é
- Encontre a expressão da intensidade do campo magnético em pontos próximos à superfície da fita. Considerando que a largura da fita é , e a corrente vale , qual o valor do campo magnético.
Passo 1
Oi, tudo bem?
Letra a)
O problema disse que há uma fita metálica que conduz corrente e pediu o campo magnético próximo a ela. Para calcular esse campo a ideia é bem simples: aplicar a lei de Ampére! Precisamos identificar um caminho que contenha toda a corrente dentro e calcular o !
Beleza?
Mas calma, vou fazer passo a passo com você!
Passo 2
Na letra (a) o problema pediu para calcularmos o campo magnético nos pontos próximos à superfície da fita, então vamos dizer que um caminho que tenha uma espessura e uma largura , de forma que e que dentro desse caminho esteja toda a fita metálica:
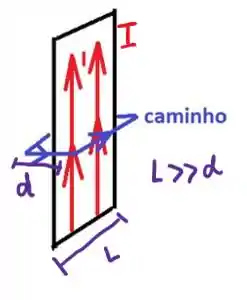
Como o problema não diz o sentido da corrente, assumi que seria vertical para cima. Sendo assim, o caminho tem perímetro , e a lei de Ampére fornece o campo ao longo desse caminho:
Certo?
E dentro desse caminho está contida toda fita, então nela passa toda corrente! Sendo assim, a lei de Ampére nos dá o campo em função da corrente contida dentro do caminho (que no nosso caso é só )
Tudo bem até aqui?
Passo 3
Lá no começo do passo 2, assumimos no nosso caminho que , e essa parte é muito importante!
Isso porque quando juntamos as duas partes da lei e fazemos a correspondência do campo com a corrente
Se considerarmos que , então o campo magnético fica em termos apenas da largura da fita:
Passo 4
E agora com os valores dados de largura e de corrente, podemos calcular o campo:
, e a corrente vale
Assim o campo é:
Ufa! Terminamos!
Bora para a próxima?