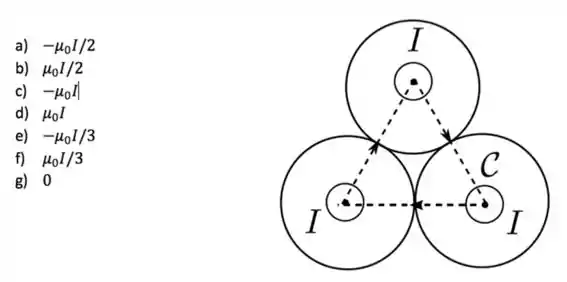
Três cilindros condutores, circulares, retos, infinitos e idênticos são posicionados de forma que seus eixos são paralelos e cada um toca os outros dois. Suas seções transversais são mostradas na figura abaixo. Cada um dos cilindros é atravessado por uma corrente estacionária de mesma intensidade , uniformemente distribuída sobre suas seções transversais, fluindo para fora do plano do papel. Considere a curva fechada mostrada na figura, formada por um triângulo cujos vértices coincidem com os eixos dos cilindros nesta seção. A circulação do campo magnétio através de , definida por , é dada por:
Passo 1
A primeira coisa importante aqui, pessoal, é se lembrar da lei de Ampère. Se ela não vem à sua cabeça logo de cara, vamos discutir um pouco disso aqui daí depois você treina um pouco mais aqui com nosso material sobre a lei de Ampère
A lei de Ampère afirma que
em que é a corrente que passa no interior da área delimitada pela curva fechada . Por exemplo, na figura abaixo, a gente só precisa considerar as correntes que passam no interior da porção delimitada pelos ângulos desenhados. A corrente que passa no restante dos cilindros fora dessa curva não entram na expressão acima, o que facilita bastante nosso trabalho.
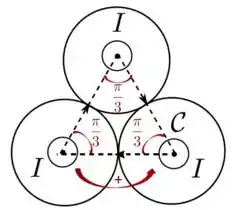
Então, para o cálculo da circulação , podemos nos focar apenas em calcular a corrente em uma dessas porções com ângulo e multiplicar por 3 e tomar bastante atenção com relação ao sentido da corrente e com o sentido da curva fechada . Vamos fazer isso agora...
Passo 2
Antes de calcular essa corrente, precisamos ver algo sobre o sinal da corrente! Todas as correntes da figura estão saindo do plano da página, blz? Isso significa que o sentido positivo é anti-horário, o que a gente pode perceber pela regra da mão direita, ok?
Agora, repara bem na figura que a curva fechada está no sentido oposto ao daquele dado pela regra da mão direita, como mostrado na figura com a seta em vermelho. Isso significa, galera, que a corrente que a gente vai contabilizar na lei de Ampère é negativa. Fechou?
Passo 3
Agora sim vamos ver qual corrente entra na nossa conta...
Como a corrente está distribuída uniformemente nos 3 cilindros, significa que em cada porção dos cilindros passa da corrente que passa no cilindro todo, correto?
Então, a corrente que no lado direito da lei de Ampère é: !!
Segue daí que, junto como sinal negativo que discutimos no Passo 2, temos que a circulação do campo magnético é dada por
Resposta
Portanto, a letra a) é a resposta correta.