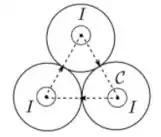
Três cilindros condutores, circulares, retos, infinitos e idênticos são posicionados de forma que seus eixos são paralelos e cada um toca os outros dois. Suas seções transversais são mostradas na figura abaixo. Cada um dos cilindros é atravessado por uma corrente estacionária de mesma intensidade , uniformemente distribuída sobre suas seções transversais, fluindo para fora do plano da página. Considere a curva fechada e orientada mostrada na figura, formada por um triângulo cujos vértices coincidem com os eixos dos cilindros nesta seção. A circulação do campo magnético através de , definida por , é dada por
a)
b)
c)
d)
e)
Passo 1
Fala galerinha, beleza?
Para resolver esse problema, você precisa lembrar da lei de Ampere:
A integral de linha do campo magnético em um caminho fechado é igual a vezes a corrente que atravessa a superfície limitada por esse caminho.
No caso, o caminho é o triângulo equilátero mostrada na figura. Como a corrente está distribuída uniformemente nos cilindros, precisamos computar a corrente que atravessa por dentro do triângulo, pintada na figura a seguir
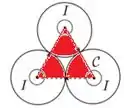
Note que a região pintada corresponde a área de três setores circulares de , correspondendo a um setor circular de (um semicírculo), cuja área é
Passo 2
A corrente que atravessa essa região é
onde é a densidade de corrente no cilindro dada por
Portanto,
Passo 3
Estamos quase finalizando o problema, só resta achar o sinal da circulação. Repare que a curva é percorrida no sentido horário, de modo que pela regra da mão direita a orientação positiva é para dentro da tela. Repare que a corrente está apontando para fora, de modo que a circulação é negativa:
Daí, é só assinalar a ALTERNATIVA E!
Resposta
Alternativa E.