Uma bola 1 de raio desprezível e massa encontra-se suspensa na extremidade de um fio inextensível, de massa desprezível e comprimento . Ela é atingida por uma bola 2,também de raio desprezível, de massa que desloca-se com velocidade , sobre uma canaleta horizontal, cuja extremidade encontra-se na posição da bola 1, como ilustrado na figura. A colisão é elástica.
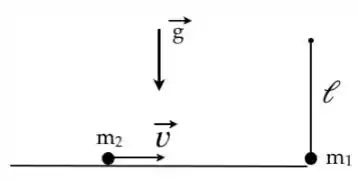
(a) Determine os vetores velocidade das bolas imediatamente após a colisão.
(b) Determine o vetor velocidade da bola 1 no topo da trajetória.
(c) Calcule a tensão no fio quando a bola 1 está no topo da trajetória.
(d) Calcule o vetor momento angular do sistema em relação ao ponto de suspensão da bola 1 antes e imediatamente após a colisão.
Passo 1
(a)
Como a colisão é elástica, podemos aplicar conservação de momento linear e conservação de energia cinética para os instantes imediatamente antes e imediatamente após essa colisão.
Aplicando conservação de momento linear:
Como antes da colisão a bola 1 está em repouso, ou seja, não possui momento linear. A equação ficará:
Aplicando conservação de energia cinética:
Agora temos um sistema de equações:
Vamos tentar resolver por substituição.
Da primeira equação:
Agora podemos substituir isso na segunda equação para encontrar o valor de .
Substituindo:
Dividindo tudo por .
Substituindo os dados do problema:
Finalmente, que conta gigantesca. Vamos substituir agora, lá naquela nossa primeira equação do sistema, para achar .
Agora precisamos definir um sistema de referencial para escrever nosso resultado.
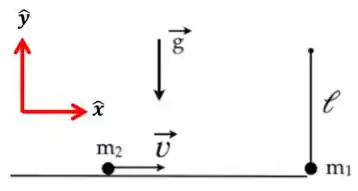
Nossa resposta ficará então:
Passo 2
(b)
Fazendo a conservação da energia mecânica:
Como a bola parte do solo, a altura inicial é nula, e ficará apenas:
A altura final nada mais é que duas vezes o comprimento do fio. Substituindo os valores:
Utilizando o referencial adotado, a velocidade final será:
Passo 3
(c)
A força resultante no topo da trajetória deve ser a força centrípeta responsável pela massa mover-se num círculo de raio . Logo:
Lembrando que , a equação ficará:
Logo:
Substituindo os dados:
Passo 4
(d)
Imediatamente antes da colisão, podemos escrever o vetor momento angular como:
Analogamente, podemos escrever para o instante imediatamente posterior à colisão. Entretanto, agora temos duas bolas em movimento, então teremos que considerar dois momentos angulares:
Resposta
(a) ;
(b)
(c)
(d) ;