44. Um sistema formado por dois baldes e uma barra estão fixados a um eixo como indicado na figura. O sistema, que gira em torno do eixo com uma certa velocidade angular, descreve um círculo no plano perpendicular ao eixo. De repente começa a chover. Despreze qualquer tipo de atrito e força de resistência. Pode-se afirmar que:
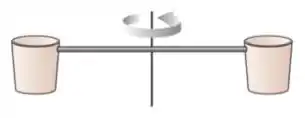
(a) Os baldes continuam girando com a mesma velocidade angular constante como consequência da conservação do momento angular do sistema baldes+barra+chuva.
(b) Os baldes giram com maior velocidade angular porque o momento angular do sistema baldes+barra é conservado.
(c) Os baldes giram com menor velocidade angular como consequência da conservação do momento angular e da energia mecânica do sistema baldes+barra+chuva.
(d) Os baldes giram com menor velocidade angular porque o momento angular do sistema baldes+barra+chuva é conservado.
Passo 1
E aí! Suave na nave?! Tá difícil essa questão? Relaxa que a gente vai te ajudar!

Nesse problema temos dois baldes que são ligados por uma barra e giram em torno do centro da barra. Então começa a chover e queremos saber o que acontece com a velocidade angular e porque acontece.
Parece difícil? 🤔
Pra resolver o problema podemos analisar o sistema como um sistema de massa variável.
Como não há perdas no sistema, podemos dizer que a energia inicial é igual a energia final.
Bora lá! 😬
Passo 2
Como em um sistema de massa variável e sem perdas de energia, podemos dizer primeiramente que o momento angular do sistema é conservado, ou seja
O momento angular pode ser calculado como
Portanto
Podemos dizer que o momento de inercia do sistema é dado genericamente por
Em que é uma constante que não nos interessa
No início os baldes estão vazios, então podemos definir uma massa imaginaria para o sistema.
Porém, quando começa a chover, os baldes enchem de água e assim podemos definir uma massa ao sistema, onde , ou seja
Como , a razão , logo
Isso significa que o sistema perde velocidade angular por conta da conservação do momento angular!
O que achou? Foi de boa? Responde aí! 😊

Resposta
(d) Os baldes giram com menor velocidade angular porque o momento angular do sistema baldes+barra+chuva é conservado.