Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Potencial Elétrico Gerado por Corpos Extensos

Ver Teoria
Exercício 124123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

PUC-RIO – Física 3 2020.1 – P3– Questão 4

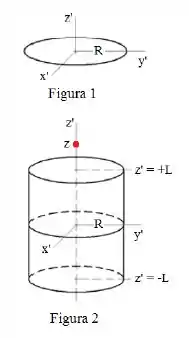
O anel de raio R mostrado na Figura 1 contém uma carga total q uniformemente distribuída.

a) Determine uma expressão para o potencial elétrico devido ao anel em um ponto qualquer do eixo z ’ ;

b) Determine o potencial elétrico devido à casca cilíndrica de r a i o   R e a l t u r a   2 L carregada com uma densidade superficial de carga σ   ( A / m 2 ) uniforme, mostrada na Figura 2, no ponto z ( >   L ) do mesmo eixo;

R   e altura   2 L carregada com uma densidade superficial de carga σ   ( A / m 2 )     uniforme, mostrada na Figura 2, no ponto z   ( >   L ) do mesmo eixo.

Passo 1

Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?

Letra (a):

O diferencial do potencial elétrico no ponto z ' devido a um elemento de carga d q situado no anel é:

d V z ' = 1 4 π ϵ 0 d q r = 1 4 π ϵ 0 d q z ' 2 + R 2 1 / 2

Logo, o potencial elétrico nesse ponto é a integral em toda carga:

∫ a n e l d V z ' = V z ' = 1 4 π ϵ 0 q z ' 2 + R 2 1 / 2

Passo 2

Letra (b):

Agora vamos considerar um anel elementar paralelo à base da casca esférica, de altura d z ' e situado na altura z ' . A carga deste anel elementar é d q = σ ( 2 π R d z ' ) . Assim, com base na resposta que a gente achou no item anterior, o diferencial do potencial elétrico é:

d V z ' = 1 4 π ϵ 0 d q r = 1 4 π ϵ 0 σ ( 2 π R d z ' ) ( z - z ' ) 2 + R 2 1 / 2

E o potencial pode ser determinado integrando essa expressão entre os limites – L até + L :

∫ - L L d V z ' = ∫ - L + L 1 4 π ϵ 0 σ ( 2 π R d z ' ) ( z - z ' ) 2 + R 2 1 / 2

E usando uma tabela de integrais chegamos a :

V z = σ R 2 ϵ 0 ln ⁡ z + L + z + L 2 + R 2   – ln ⁡ z - L + z + L 2 + R 2      

Tranquilo? Vamos para o último item?

Passo 3

Letra (c):

E agora o campo elétrico pode ser encontrado derivando o potencial em relação a z :

E → = - d V d z z ^

E → = σ R 2 ϵ 0 1 + 1 2 2 z - L z - L 2 + R 2 z - L 2 + R 2 - 1 + 1 2 2 z + L z + L 2 + R 2 z + L 2 + R 2  

E → = σ R 2 ϵ 0 1 z - L 2 + R 2 - 1 z + L 2 + R 2 z ^

Beleza?

Pronto pra próxima questão? =)

Resposta

a ) V z ' =   1 4 π ϵ 0 q z ' 2 + R 2 1 / 2

b ) V z = σ R 2 ϵ 0 ln ⁡ z + L + z + L 2 + R 2   – ln ⁡ z - L + z + L 2 + R 2      

c ) E → = σ R 2 ϵ 0 1 z - L 2 + R 2 - 1 z + L 2 + R 2 z ^

Exercícios de Livros Relacionados

Uma barra de plástico tem a forma de um circunferência de raio R = 8,20 cm. A barra possui uma carga Q 1 = +4,20 pC uniformemente distribuída ao longo de um quarto de circunferência e uma carga Q 2 =
A Fig. abaixo mostra uma barra fina de plástico que coincide com o eixo x. A barra tem um comprimento L = 12,0 cm e uma carga positiva uniforme Q = 56,1 fC uniformemente distribuída. Com V= 0 no infin
O rosto sorridente da Fig. Abaixo é formado por três elementos: 1: Uma barra fina com uma carga de -3,0μ C e a forma de uma circunferência completa com 6,0c m de raio; 2: Uma segunda barra fina com um
Qual é o módulo do campo elétrico no ponto 3,00 i ^ - 2,00 j ^ + 4,00 k ^ m se o potencial elétrico é dado por V = 2 x y z 2 , em que V está em volts e x, y e z estão em metros?
Um elétron é colocado no plano xy, onde o potencial elétrico varia com x e y de acordo com os gráficos da figura abaixo (o potencial não depende de z) . Em termos dos vetores unitários, qual é a força