O anel de raio mostrado na Figura contém uma carga total uniformemente distribuída. O potencial elétrico devido ao anel em um ponto qualquer do eixo é:
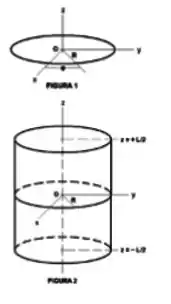
(a) Use o resultado acima para determinar uma expressão para o potencial elétrico em um ponto arbitrário do eixo devido a um disco de raio carregado com a densidade superficial , onde é a distância de um ponto do disco ao seu centro (Figura ).
Suponha agora que a casca cilíndrica da Figura seja longa e que os pontos de interesse sejam externos a ela e próximos da sua superfície, mas afastados de suas extremidades.
(b) Determine o vetor campo elétrico em um ponto de interesse arbitrário, em função da distância ao eixo da casca cilíndrica.
(c) Use o resultado do item anterior para determinar a diferença entre os potenciais elétricos (ddps) de pontos de interesse situados em e .
Passo 1
(a) O disco será subdividido em anéis de espessura . A carga de um anel de raio será . Portanto, a contribuição do anel de raio para o potencial elétrico no ponto arbitrário do eixo é:
Portanto, para achar o potencial resultante, devemos integrar:
Essa integral é um pouco complicada, mas uma integral por partes resolve ela, resultando em:
Simplificando:
Passo 2
(b) Supondo uma superfície Gaussiana cilíndrica de altura e raio , cujo eixo coincide com o da casca, obtém-se:
Sabendo que, quando a carga interna será nula, temos, reorganizando:
Passo 3
(c) Queremos:
Fazendo a integração do campo elétrico entre esses dois raios:
Agora substituindo a expressão de campo elétrico que encontramos no item anterior:
Integrando:
Portanto:
Resposta
a)
b)
c)