Uma barra fina e isolante de comprimento é posicionada sobre o eixo de um sistema de coordenadas com seu centro sobre a origem, como mostrado na figura abaixo.

Ela possui uma densidade linear de carga não-uniforme dada por , onde é uma constante positiva. Considere que o potencial elétrico é nulo no infinito.
Determine o potencial elétrico em um ponto sobre o eixo , a uma distância da origem.
Obtenha uma expressão assintótica para o resultado do item no limite . Interprete o resultado.
No formulário tem essa integral simpática (nem tanto):
E também tem essa aproximação:
Passo 1
Determine o potencial elétrico em um ponto sobre o eixo , a uma distância da origem.
A estratégia pra esse tipo de problema é começar pegando um pedaço muito pequeno da barra, com uma carga infinitesimal , se liga:
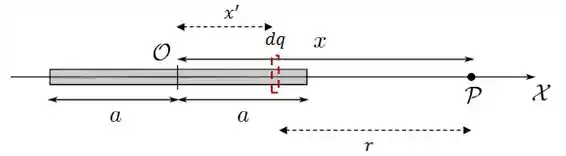
O potencial gerado por esse pedaço infinitesimal será:
Onde podemos associar a carga infinitesimal à densidade linear de carga da seguinte forma:
Além disso, a distância pode ser escrita como:
Dessa forma, substituindo esses caras na expressão de , temos que:
Passo 2
O que temos que fazer agora é integrar essa expressão, onde .
Algumas vezes a gente pode acabar travando na integral, então quando aparecer algo que você não esteja acostumado, dê uma olhada no formulário, porque a resolução dessa integral pode estar lá (o que acontece no caso dessa prova).
Então, de acordo com o formulário:
Obs.: Coloquei o sinal negativo na frente da integral pra que o denominador ficasse mais parecido com o que aparece no formulário.
Substituindo na expressão do potencial e aplicando os limites de integração, teremos:
Agora é só arrumar a bagunça:
Passo 3
Obtenha uma expressão assintótica para o resultado do item no limite . Interprete o resultado.
Ok! Para tratar do caso a que o problema se refere, temos que começar olhando para a parte logarítmica da expressão do potencial, isso porque ela relaciona e .
De acordo com o enunciado, há uma aproximação que podemos fazer com um logaritmo muito semelhante a esse, se liga:
Então a ideia aqui é a seguinte, vamos transformar o logaritmo que aparece na expressão do potencial nesse cara aqui em cima.
Opa! Sendo , podemos dizer que:
Agora sim, podemos aplicar a aproximação que o formulário no deu:
Feito isso, agora podemos substituir na expressão do potencial:
Vamos arrumar essa bagaça:
Finalmente:
Passo 4
Agora temos que interpretar esse resultado! Fisicamente se , quer dizer que se estamos muito afastados da barra enxergamos ela como um ponto!
Se você lembrar da densidade de carga
Vai ver que pra , e que pra , , ou seja, essa nossa barra é um dipolo elétrico! Como estamos vendo bem de longe, temos um dipolo elétrico pontual.
Lembra como era a expressão do campo produzido por um dipolo elétrico?
E o potencial então é dado por (lembrando que )
Que tem a mesma cara que a expressão que a gente achou! Ou seja, pra distâncias muito grandes a nossa barra se comporta como um dipolo pontual!
Resposta
Análise: Ver passo 4.