Considere a coroa circular da figura 1, raio interno e raio externo , com densidade superficial de carga não uniforme dada pela função , onde é uma constante positiva e é a distância a partir do centro. Considere também o ponto no eixo da coroa, à altura do centro. A figura 2 mostra um anel de raio e carga total . Sabe-se que o potencial geral em pelo anel é dado por
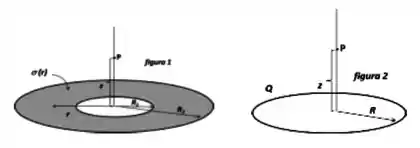
a) Adaptando o resultado do potencial do anel, utilize a relação para encontrar o potencial gerado pela coroa circular em .
Suponha, agora, que uma carga pontual , inicialmente em repouso no ponto , é solta e cruze a origem , submetida à força elétrica (desconsidere, portanto, a força de gravidade).
b) Para que isso aconteça, que sinal deve ter a carga e qual será a sua energia cinética final ao cruzar a origem?
Desconsidere, agora, a carga e suponha que o potencial geral pela coroa circular em tenha o seguinte valor: . Imagine uma casca esférica isolante de espessura infinitesimal seja colocada envolvendo toda a coroa circular e também o ponto . A casca esférica possui uma carga uniformemente distribuída em sua superfície.
c) Calcule que raio a casca esférica deve ter para que o potencial total em seja nulo. (Considere ).
Passo 1
a)
Utilizando a integral fornecida na capa da prova, ficamos com:
Passo 2
b)
- Como a carga da coroa é positiva, uma carga só pode se aproximar dela se for negativa.
- Como só existe a força elétrica, o sistema é conservativo. Logo:
Utilizando a expressão que encontramos no item anterior para o potencial, chegamos a
que resulta em
Simplificando
Passo 3
c) O potencial em todos os pontos no interior de uma casca uniformemente carregada é constante e vale
Como precisamos anular o potencial de gerado pela coroa, é preciso que: