Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Potencial Elétrico Gerado por Corpos Extensos

Ver Teoria
Exercício 131123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFJF – Física 3 – AV1 – 2014.1 – Questão 2b

Considere um disco de plástico perfurado de raio menor a e raio maior b , uniformemente carregado com uma densidade de carga σ :

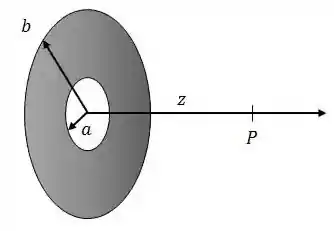
(b) Calcule o campo elétrico em P .

Passo 1

Eaee!!! Belezinha? Bom... a questão nos dá um disco de plástico carregado uniformemente com uma densidade de carga σ .

A questão nos pede para calcular o campo elétrico gerado por esta distribuição no ponto P mostrado na figura.

Lembrando que o campo elétrico E é calculado da seguinte forma:

E = ∫ k d 2   d Q

Onde k é a constante eletrostática, d Q é um elemento de carga infinitesimal sobre o disco e d é a distância entre o elemento de carga e o ponto P .

E aí? Bora responder?

Passo 2

Bom... por simetria, observa-se que o campo elétrico gerado pelo disco de cargas no ponto P produz resultante apenas no eixo perpendicular ao disco, como mostrado a seguir:

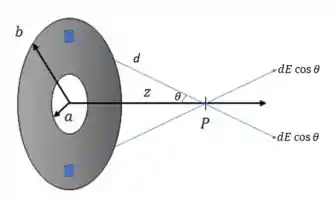
Passo 3

Dessa forma, temos para o campo elétrico resultante, de forma análoga a alternativa (a):

E = ∫ a b k d 2 d Q cos ⁡ θ ∴

E = ∫ a b k d 2 cos ⁡ θ σ 2 π r   d r   z d ∴

E = σ 2 π r k z ∫ a b r r 2 + z 2 3 d r ∴

E = 2 k σ π z - 1 r 2 + z 2 b a ∴

E = 2 k σ π z 1 a 2 + z 2 - 1 b 2 + z 2

Entendeu direitinho? Responde aee ;)

Resposta

E = 2 k σ π z 1 a 2 + z 2 - 1 b 2 + z 2

Exercícios de Livros Relacionados

Uma barra de plástico tem a forma de um circunferência de raio R = 8,20 cm. A barra possui uma carga Q 1 = +4,20 pC uniformemente distribuída ao longo de um quarto de circunferência e uma carga Q 2 =
A Fig. abaixo mostra uma barra fina de plástico que coincide com o eixo x. A barra tem um comprimento L = 12,0 cm e uma carga positiva uniforme Q = 56,1 fC uniformemente distribuída. Com V= 0 no infin
O rosto sorridente da Fig. Abaixo é formado por três elementos: 1: Uma barra fina com uma carga de -3,0μ C e a forma de uma circunferência completa com 6,0c m de raio; 2: Uma segunda barra fina com um
Qual é o módulo do campo elétrico no ponto 3,00 i ^ - 2,00 j ^ + 4,00 k ^ m se o potencial elétrico é dado por V = 2 x y z 2 , em que V está em volts e x, y e z estão em metros?
Um elétron é colocado no plano xy, onde o potencial elétrico varia com x e y de acordo com os gráficos da figura abaixo (o potencial não depende de z) . Em termos dos vetores unitários, qual é a força