UFJF – Física 3 – AV1 – 2014.1 – Questão 2a
Considere um disco de plástico perfurado de raio menor e raio maior , uniformemente carregado com uma densidade de carga :
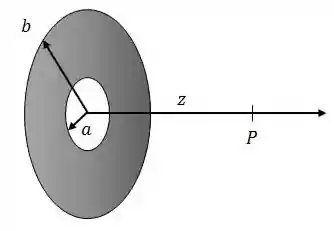
(a) Calcule o potencial elétrico gerado por esta distribuição em um ponto sobre o eixo de simetria perpendicular ao plano que contém o disco e passa por seu centro geométrico. Tome o potencial no infinito como zero!
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá um disco de plástico carregado uniformemente com uma densidade de carga .
A questão nos pede para calcular o potencial elétrico gerado por esta distribuição no ponto mostrado na figura.
Lembrando que o potencial elétrico é calculado da seguinte forma:
Onde é a constante eletrostática, é um elemento de carga infinitesimal sobre o disco e é a distância entre o elemento de carga e o ponto .
E aí? Bora responder?
Passo 2
Bom... considerando o elemento de carga sobre o disco, a sua distância até o ponto é dada por:
Onde é a distância entre o centro do disco e o elemento de carga e é a distância entre o centor e o ponto .
Sendo assim, o potencial elétrico no ponto é dado da seguinte forma:
Passo 3
Sabe-se, no entanto, que o elemento de carga pode ser tratado como o produto entre a densidade de carga e um elemento de área . Ou seja:
Onde é dado por (ver figura abaixo):
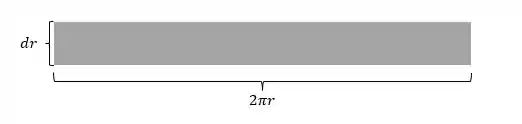
Assim, o elemento de carga é dado da seguinte forma:
Passo 4
Substituindo a integral e resolvendo para variando de até , temos:
Entendeu direitinho? Responde aee ;)
