Considere um disco de raio com uma carga uniformemente distribuída.
a) Calcule o potencial num ponto do eixo do disco, a uma distância do centro.
b) Qual é a diferença de potencial entre o centro do disco e um ponto sobre seu eixo a uma distância do centro?
c) Utilizando a relação entre campo elétrico e o potencial, deduza uma expressão para o campo elétrico do disco no ponto do item (a).
d) Qual é o trabalho necessário para trazer uma carga de prova desde o infinito até o centro do disco?
Dado: potencial de um anel com carga , em um ponto do eixo do anel, a uma distância do centro:
Passo 1
a) Nessa questão o enunciado já deu uma dica muito boa: ele deu o potencial gerado no ponto por um anel:
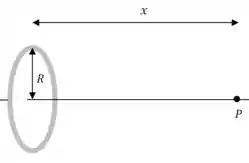
Mas presta atenção num detalhe: um disco é simplesmente um conjunto de anéis!
Outra forma de dizer isso é considerar que cada anel de raio contribui com um potencial para o potencial do disco:
E como a gente pode expressar essa “carguinha” de cada anel? Bom, se o disco inteiro tem carga e área , a densidade de carga é:
E então a carga de cada disco é:
E como , :
Ou seja:
Beleza, já estamos quase lá.
Passo 2
Agora, pra encontrar o potencial gerado pelo disco, é só integrar esse conjunto de anéis:
Com variando de até :
Tirando as constantes:
E usando essa fórmula aqui:
Ou seja:
Como :
Substituindo :
Então o potencial devido ao disco é:
Passo 3
(b) Quando estamos no centro do disco, o potencial é :
E quando estamos a uma distância do centro:
Cortando o :
Então a diferença de potencial entre os dois pontos é:
Passo 4
(c) Agora queremos descobrir o campo elétrico do disco no ponto .
Não tem segredo, é só lembrar da relação do campo elétrico com o potencial:
O campo elétrico é o gradiente do potencial! Se a gente olhar só para o campo ao longo do eixo , esse gradiente é:
Então:
Primeiro vamos tirar as constantes:
Agora podemos separar a derivada em duas:
A primeira derivada, pela regra da cadeia, fica assim:
E a segunda é bem mais simples, já que o ponto está em , ou seja, :
Então:
Já que o enunciado também chama de a posição do ponto , essa é a expressão que estávamos procurando!
Passo 5
(d) Agora vamos lembrar da relação entre o trabalho e a variação de potencial:
Se vamos até no centro do disco vindo de no infinito:
E já calculamos :
E o potencial é zero no infinito, então:
Resposta
(a) O potencial em é .
(b) A diferença de potencial é .
(c) O campo elétrico em é .
(d) O trabalho realizado para isso é .