Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Potencial Elétrico Gerado por Corpos Extensos

Ver Teoria
Exercício 118123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Campo Elétrico, Potencial Elétrico

Considere o gráfico da figura abaixo.

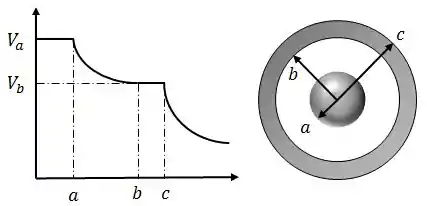
Ele corresponde ao potencial elétrico em função da distância à origem de um sistema de cargas com simetria esférica e raio externo c . Para este sistema, responda:

  1. Qual a intensidade do campo elétrico para b < r < c ?
  2. Qual a carga total do sistema?
  3. Qual o campo elétrico para r > c em função de r e das grandezas fornecidas?

Passo 1

  1. Qual a intensidade do campo elétrico para b < r < c ?

    2. Podemos associar o campo elétrico com o potencial através da relação:

    Δ V = - ∫ C   E → ∙ d r →

    E = - d V d r

    Assim, temos como descobrir a intensidade do campo elétrico analisando a tangente da curva.

    Na região b < r < c :

    d V d r = 0

    Logo:

    E = 0

    Passo 2

  2. Qual a carga total do sistema?

    3. Vamos lá, o potencial elétrico de uma carga é dada por:

    V r = 1 4 π ϵ 0 q r = k q r

    A distância r que engloba todo o sistema é r = c . Para esse valor, o potencial elétrico vale V b .

    Logo:

    V b = 1 4 π ϵ 0 q c

    q = 4 π ϵ 0 c V b

    Passo 3

  3. Qual o campo elétrico para r > c em função de r e das grandezas fornecidas?

Para r > c , o sistema se comporta como uma carga pontual de valor q . Portanto, quando r > c , o campo elétrico é dado por:

E r = 1 4 π ϵ 0 q r 2

E r = 4 π ϵ 0 c V b 4 π ϵ 0 r 2

E r = c V b r 2

Resposta

a.

E = 0

b.

q = 4 π ϵ 0 c V b

c.

E r = c V b r 2

Exercícios de Livros Relacionados

Uma barra de plástico tem a forma de um circunferência de raio R = 8,20 cm. A barra possui uma carga Q 1 = +4,20 pC uniformemente distribuída ao longo de um quarto de circunferência e uma carga Q 2 =
A Fig. abaixo mostra uma barra fina de plástico que coincide com o eixo x. A barra tem um comprimento L = 12,0 cm e uma carga positiva uniforme Q = 56,1 fC uniformemente distribuída. Com V= 0 no infin
O rosto sorridente da Fig. Abaixo é formado por três elementos: 1: Uma barra fina com uma carga de -3,0μ C e a forma de uma circunferência completa com 6,0c m de raio; 2: Uma segunda barra fina com um
Qual é o módulo do campo elétrico no ponto 3,00 i ^ - 2,00 j ^ + 4,00 k ^ m se o potencial elétrico é dado por V = 2 x y z 2 , em que V está em volts e x, y e z estão em metros?
Um elétron é colocado no plano xy, onde o potencial elétrico varia com x e y de acordo com os gráficos da figura abaixo (o potencial não depende de z) . Em termos dos vetores unitários, qual é a força