Um disco de raio oco, de raio interno e raio externo conforme mostrado na figura abaixo, possui uma distribuição superficial de carga expressa por , onde é uma constante com unidade de carga por unidade de área.
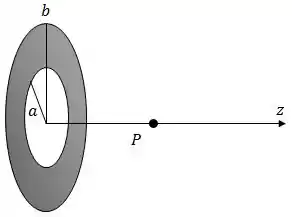
Dado:
Determine:
A carga total no disco, em função de e ;
O potencial elétrico sobre o eixo do disco a uma distância de seu centro;
A energia potencial elétrica necessária para colocar uma carga , num ponto de coordenada ao longo do eixo do disco a uma distância , trazida do infinito;
Passo 1
A carga total no disco, em função de e ;
Por definição, a densidade superficial de carga pode ser escrita por:
Onde corresponde a área de um pedaço infinitesimal do disco, de carga .
Como a área de uma seção circular é dada por , o elemento será dado por:
Além disso, o problema nos disse que a densidade superficial de carga é dada por:
Substituindo e na expressão de , teremos:
Finalmente, pra calcular a carga total, só temos que integrar esse cara de até :
Passo 2
O potencial elétrico sobre o eixo do disco a uma distância de seu centro;
A ideia aqui é começar calculando o potencial elétrico gerado por uma carga infinitesimal . Esse potencial é dado por:
Obs.: Chamei a distância de só pra diferenciar do que usamos no item , beleza?
Graficamente, a ideia é essa:
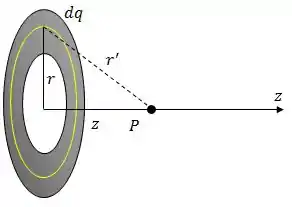
Daqui já conseguimos tirar algumas coisas:
Substituindo esses caras na expressão de , teremos:
Simplificando:
Passo 3
Pra finalizar, só temos que integrar esse cara de até :
Opa! Não precisa quebrar a cabeça calculando essa integral! O próprio enunciado já deu a resposta dela... só temos que adaptar.
Passo 4
A energia potencial elétrica necessária para colocar uma carga , num ponto de coordenada ao longo do eixo do disco a uma distância , trazida do infinito;
Por definição, o potencial elétrico está associado com a energia potencial elétrica por:
O potencial no infinito é nulo!
Portanto:
Resposta