Uma esfera metálica carregada com uma carga se situa dentro de uma casca esférica condutora com carga . A esfera interna possui raio e a casca externa possui raio , com . O espaço entre as esferas é o vácuo.
a) Calcule o potencial elétrico em todos os pontos.
b) Desenhe o gráfico do potencial, destacando valores em relação a cada um dos corpos.
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu uma esfera metálica carregada dentro de uma esfera condutora e pediu pra gente calcular o potencial elétrico em todos os pontos. Mas que pontos são esses?
Vamos desenhar as duas esferas pra enxergar melhor:
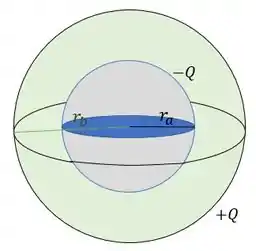
Como a nossa esfera interna tem raio e a esfera externa tem raio , vamos definir três regiões, pra englobar todos os pontos e calcular o potencial elétrico: dentro da esfera mais interna, onde o raio é , entre as duas esferas () e fora da esfera externa ().
Lembra da expressão pra calcular o potencial? É essa daqui:
Com essas informações a gente consegue calcular o potencial em todos os pontos e, em seguida, desenhar o gráfico do potencial.
Vamos lá!
Passo 2
Galera, vamos começar calculando o potencial dentro das duas esferas, onde . Assim, temos:
Colocando em evidência:
Agora para , onde estamos fora da esfera interna e dentro da esfera externa. Temos:
E finalmente, para , quando estamos fora das duas esferas:
Passo 3
Prontinho, agora podemos desenhar o gráfico do potencial em relação a cada um dos corpos.
Por meio das equações que encontramos, podemos dizer que o potencial elétrico é inversamente proporcional à distância entre um ponto e a carga fonte . Dessa forma, o gráfico do potencial é uma hipérbole equilátera no primeiro quadrante, se for positiva.
Pra nossa esfera então, temos:
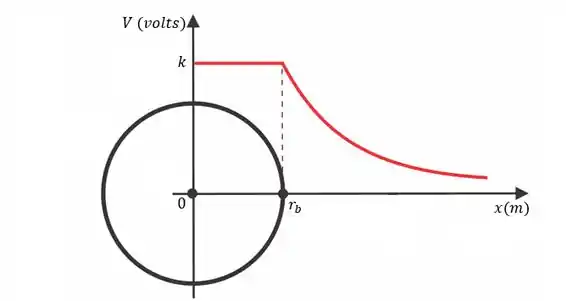
E encerramos o exercício. Valeu, galera! 😉