Lei de Gauss, Campo em Condutores, Potencial Elétrico
Uma esfera não condutora de raio carregada com uma carga , uniformemente distribuída por todo seu volume, é envolvida por uma camada esférica condutora, raios e , carregada com uma carga total , conforme a figura.
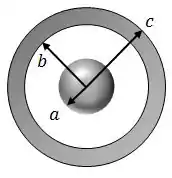
- Use a lei de Gauss para determinar as expressões do vetor campo elétrico em todo espaço: , , e ;
- Calcule a diferença de potencial entre um ponto da superfície da esfera e um ponto da superfície interna da camada, isto é, ;
- Quais são as cargas sobre as superfícies interna e externa da camada condutora?
Passo 1
- Use a lei de Gauss para determinar as expressões do vetor campo elétrico em todo espaço: , , e ;
- Calcule a diferença de potencial entre um ponto da superfície da esfera e um ponto da superfície interna da camada, isto é, ;
- Quais são as cargas sobre as superfícies interna e externa da camada condutora?
A lei de Gauss é dada por:
Como a geometria do problema é esférica... em todos os casos aqui a nossa gaussiana vai ser uma esfera. Isso significa que podemos simplificar a Lei de Gauss para:
É importante dizer também que o campo elétrico está na direção radial. Assim, só dependemos do sinal da carga interna pra saber se o campo elétrico está apontando para dentro ou para fora.
Isso significa que, para cada região, só vamos ter o trabalho de calcular .
Passo 2
-
Como a esfera é não condutora, significa que as cargas estão distribuídas ao longo do seu volume. Então, pra descobrir , basta fazer uma regra de três:
Logo:
-
Nessa região, a carga interna será a carga total da esfera não condutora, logo:
-
Beleza! Como a casca é condutora, tem uma coisa muito importante que você precisa levar contigo no coração... o campo elétrico no interior de um condutor será sempre igual a zero!
Logo:
-
Nesse caso, a carga interna total será a soma da carga da esfera não condutora e da casca condutora.
Logo:
Passo 3
Na letra (a), nós vimos que o campo elétrico na região entre a esfera e a camada condutora é dado por:
Podemos associar a diferença de potencial com o campo elétrico através da relação:
Logo:
Passo 4
- Camada interna:
Lembra que, quando calculamos o campo elétrico no interior do condutor, vimos que ele será sempre nulo?
Mas, de acordo com a Lei de Gauss, o campo elétrico é dado por:
Assim, a única forma do campo elétrico ser igual a zero é se a soma das cargas internas à nossa gaussiana quando também for igual a zero.
A carga interna nessa região será a soma da carga da esfera com a carga da camada interna da casca condutora :
- Camada externa:
O problema nos disse que a casca condutora possuía carga , certo? Isso significa que, não importa a quantidade de carga na camada interna e na camada externa, desde que a soma das duas seja igual a , entendeu?
Resposta
a.
-
-
-
-
b.
c.