A figura abaixo ilustra um capacitor cilíndrico de comprimento , composto por duas cascas cilíndricas coaxiais. A casca interna tem raio e carga , e a casca externa tem raio e carga . Sabe-se que e que . Existe vácuo no espaço entre as placas (), cuja constante de permissividade elétrica é dada por .
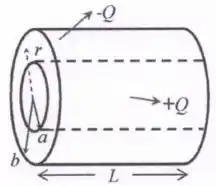
- Calcule o módulo do campo elétrico na região entre as cascas .
- Calcule a diferença de potencial elétrico entre as cascas.
- Calcule a capacitância de tal capacitor cilíndrico.
- Se o espaço entre as placas é completamente preenchido por um material dielétrico de constante dielétrica , determine a nova capacitância deste sistema.
Passo 1
a) Para o módulo do campo elétrico na região , vamos usar a lei de Gauss, que afirma o seguinte:
ou seja, o fluxo do campo elétrico através da superfície gaussiana (superfície fechada!) é igual a carga total líquida que está dentro da superfície fechada dividida por .
Bom, para usarmos a lei de Gauss para o caso da nossa questão aqui, vamos usar uma superfície gaussiana fechada cilíndrica de raio (), como a gente colocou na figura abaixo, que foi desenhada de perfil.
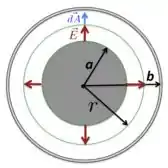
Como o enunciado disse que e (portanto também!), então temos um cilindro “infinito”: o comprimento de ambos os cilindros é muito maior do que os respectivos diâmetros. Nesse caso, o campo elétrico produzido por eles tem propriedades particulares, que vem desse simetria cilíndrica.
Por essa característica, o campo elétrico é sempre radial, ou seja, sempre perpendicular ao eixo longitudinal dos cilindros e isso significa que não tem componente do campo perpendicular às tampas da nossa superfície gaussiana. Além disso, só depende da distância ao seu eixo.
Agora, como a carga do cilindro interno é positiva, o campo elétrico que ela gera pode ser escrito como . O vetor infinitesimal de área é sempre escolhido apontando para fora da gaussiana: , sendo que está relacionada ao elemento de área lateral do da gaussiana.
Como e são paralelos e tem o mesmo valor em todos os pontos da superfície lateral da gaussiana, o lado esquerda da lei de Gauss fica:
já que a carga que está dentro da superfície gaussiana é . Isolando o campo, teremos:
Passo 2
b) Uma vez que temos o campo elétrico, podemos calcular a diferença de potencial através de
Nesse caso, podemos tomar o vetor infinitesimal de comprimento na direção radial: . Como também está na direção radial, o produto escalar na expressão acima fica: . Colocando isso na integral, teremos
Passo 3
c) Agora, basta a gente aplicar a definição de capacitância, que é
Aplicando isso na expressão que encontramos no item anterior, tiramos que a capacitância do capacitor cilíndrico será
Passo 4
d) Quando colocarmos um dielétrico preenchendo todo o volume entre os dois condutores do capacitor cilíndrico, sua nova capacitância será maior por um fator , ou seja, terá um valor dado por: