Oito gotas de água idênticas estao todas ao mesmo potencial , relativo ao potencial nulo no infinito. Elas se juntam para formar uma única gota esférica, cujo potencial deve ser:
a)
b)
c)
d)
e)
Passo 1
Bom pessoal, o primeiro passo aqui é entender como se calcula o potencial de uma gota d’água.
A ideia é a seguinte: a água é uma boa condutora de eletricidade, então a gente pode tratar a gota como uma esfera condutora carregada.
Você já deve ter visto que, pela lei de Gauss, o campo elétrico gerado por uma esfera condutora carregada segue essa fórmula aqui:
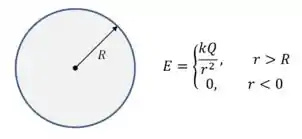
Bom, mas se o campo elétrico é nulo dentro da esfera, isso quer dizer que o potencial elétrico é constante dentro da esfera:
Beleza? Se o é zero nessa equação, então o potencial é uma constante, porque a integral de zero é uma constante!
Passo 2
Tá, o potencial é uma constante, mas qual é o valor dessa constante?
É só voltar na fórmula de antes:
Integrando isso do infinito até a superfície da esfera :
A integral de é , então:
E já que o potencial é zero no infinito:
Beleza, esse é o valor do potencial na superfície da esfera.
Como a gente viu lá em cima, o potencial é constante na esfera toda, então esse mesmo valor é a constante que estávamos procurando.
Passo 3
Então tá, a gente começa com uma única esfera (gota d’água) com potencial :
Cada uma tem carga e raio . Se a gente juntar gotas como essa, qual vai ser a carga total?
E qual vai ser o raio dessa nova gota? Aqui não dá pra simplesmente somar os raios.
O volume da nova gota é:
Vamos ver qual era o volume de uma única gota usando a fórmula para o volume de uma esfera?
Então:
Agora a gente pode calcular o raio da esfera que tem volume :
Cortando dos dois lados:
Tirando a raiz cúbica dos dois lados:
Passo 4
Ou seja, a nova gota tem carga e raio . Então o potencial é:
Então, como :
Então a resposta é a letra (b)!
Resposta
Letra (b).