Qual o potencial eletrostático no centro de um anel metálico de raio e carga ?
- .
- .
- .
- .
- .
Passo 1
Aqui, vamos desenhar o anel metálico no plano só para facilitar a visualização do que precisamos, como a gente fez na figura abaixo.
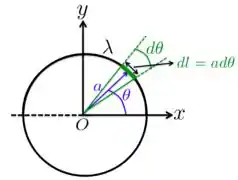
Primeiro, vamos a carga infinitesimal e calcular o potencial que ela produz no centro do anel. Já vimos que esse potencial tem a seguinte cara:
Agora, vamos imaginar uma distribuição linear de cargas . Com isso, podemos expressar o elemento de carga como . Mas, dá uma olhada na figura acima, podemos escrever esse elemento de comprimento como . Colocando tudo isso na expressão acima e integrando:
Passo 2
Daí, você deve estar se perguntando: e o , posso colocar para fora da integral? Repara que o problema não fala nada sobre o ser uniforme! Eita...kkkk
Mas não se preocupe! O ponto aqui é que o anel da questão é CONDUTOR, por isso, a carga distribuída nele é UNIFORME, ok? Como esse condutor não tem nenhuma ponta, a quantidade de cargas distribuída é a mesma em toda a extensão do anel.
Portanto, a distribuição é uniforme e é dada por
Tirando o da integral e substituindo a expressão acima, teremos:
Resposta
Letra e.