Um fio retilíneo e infinito, carregado com uma densidade linear positiva e uniforme, , é colocado no interior de uma casca cilíndrica espessa, tambéminfinita,

Condutora e neutra, de raios interno, e externo, . Determine:

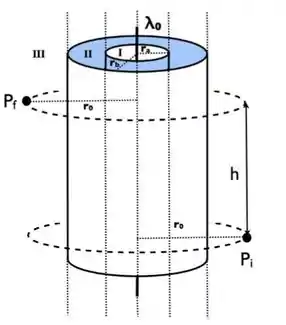
a carga contida num segmento de altura do fio,e as densidades superficiais de carga, e ,induzidas nas superfícies interna e externa do cilindro, respectivamente.

o campo elétrico, ,nas regiões

o potencial eletrostático, ,em todas as três regiões, apartir de,colocando o zero do potencial na superfície mais externado cilindro, de raio .

a.entreospontos e assinalados na figura (justifique sua resposta)

Agora vamos calcular a densidade superficial de carga na superfície interna da casca . Bem, vamos lembrar que a densidade de carga superficial é dada por:

A área da superfície interna é fácil de descobrir, área de um cilindro é

Calculando a área interna então, temos:

Feito isso, ainda falta calcular a carga na superfície interna .

Para isso, temos que lembrar do efeito de indução. O que acontece quando colocamos um objeto carregado positivamente perto de um objeto neutro?

As cargas positivas do objeto carregado vão atrair as cargas NEGATIVAS do objeto neutro, e repelir as cargas POSITIVAS, concorda?

Então quando colocamos o fio carregado positivamente dentro da casca, estamos induzindo uma carga negativa na parte interna da casca, e uma carga positiva na superfície externa. Como não houve contato, a casca continua isolada, e no inicio ela era neutra, significa que a carga total nela continua sendo , apesar da indução, Sendo assim , Guarde isso, que vamos usar ainda essa relação.

Mas, vamos voltar ao fato da carga do fio, induzir uma carga de mesmo módulo porém sinal oposto na superfície interna da casca . Assim,

Descoberto , podemos calcular a densidade de carga

Vamos calcular a densidade superficial de carga na superfície externa , lembra que vimos que a carga total da casca ainda é e para isso

Assim,

Assim, a densidade será

Feito, item resolvido, partiu parao próximo.

Vamos calcular os campos elétricos pedidos, começando pela primeira região , para isso, vamos usar a lei de Gauss.

Como nessa região temos apenas o fio, então vamos analisar o campo elétrico gerado por ele (um fio retilíneo e uniforme). Talvez você já tenha até decorado a resposta do campo dele de tanto que é cobrado, mas vamos calcular, né!?

Pela simetria apresentada por um fio, temos que seu campo é na direção Assim, podemos usar um cilindro como superfície gaussiana (as tampas terão fluxo ). Assim, resta apenas a lateral do cilindro.

A carga interna, já calculamos é a carga do fio dada uma altura . O campo é constante, então temos

Substituindo isso na equação lá de cima, temos que

Isolando o campo elétrico, chegamos em:

Agora, vamos analisar a região . Novamente iremos usar a lei de Gauss, como auxílio. Escolhendo novamente um cilindro como superfície gaussiana. Temos

Onde a carga interna será

Assim o campo elétrico nessa região é nulo, o que faz total sentido se lembrarmos que nessa região estamos dentro da casca que é um condutor, e vimos na teoria que dentro de um condutor não há ação de campo elétrico.

Já a região terá carga interna,

Tendo a mesma carga interna que a região , e quando formos usar a lei de Gauss, iríamos usar um cilindro novamente, pois a carga tem a mesma forma do fio, então, nada mudou, o campo elétrico será dado pela mesma equação do campo da região

Para acharmos o potencial dado um campo elétrico, temos que usar :

Como o enunciado pediu para que adotássemos o potencial em sendo nulo, então nossa integral começa dele e vai até o pedido.

Agora, vamos começar estudando as regiões na ordem invertida, começando pela região

Podemos passar o sinal de menos para dentro do logarítmo, pois

Assim, temos que

Observe que como , então é negativo.

Na região , já vimos que não há campo elétrico, então não haverá diferença de potencial, como em é zero, então o potencial em toda essa região também é zero.

Vale lembrar que essa região é a parte interna da casca condutora, então estamos dentro de um condutor e por isso, a teoria nos diz que o potencial no interior de um condutor é igual ao potencial em sua superfície.

Como na superfície o potencial foi adotado como nulo, então o potencial nessa região também será.

Agora, a última região , nessa região, temos um detalhe, quando escrevemos a equação

Observe que a integral vai de até , ou seja ela passa pela região , assim temos que dividir essa integral em duas, uma de até , pois o campo elétrico nessa região é diferente da região , e a outra seria de a .

Como já vimo, o potencial na região é zero, então ficamos com

Substituindo o valor do campo elétrico na região , temos

Isolando as constantes temos

Podemos fazer o mesmo lance de tirar o sinal de menos, invertendo a fração do logaritmo

Observe como nesse caso, , então é positivo.

Ambos os pontos estão na região Assim, os potenciais serão dados por:

Como os dois pontos estão equidistantes do centro, então eles possuem o mesmo potencial.

O que significa que eles estão em uma mesma superfície equipotencial.