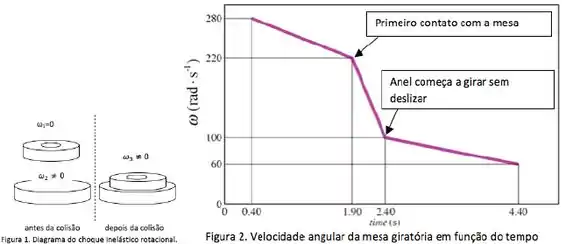
Num experimento de momento angular mostrado na foto ao lado, um anel é colocado em contato com uma mesa giratória, de tal maneira que o eixo do anel coincida com o eixo de rotação da mesa (colisão angular inelástica). Antes do contato com o anel, a mesa girava com velocidade angular decrescente por causa do atrito com os rolamentos. Durante o experimento, a velocidade angular variou conforme ilustrado no gráfico.
Assuma que:
- o anel possui o mesmo momento de inércia que o da mesa giratória em relaçao àquele eixo de rotação,
- a força de atrito entre os rolamentos e a mesa giratória é constante durante todo o movimento.
Expresse todas as suas respostas em função de e dos dados do gráfico.
a) Calcule o torque da força de atrito entre os rolamentos e a mesa giratória
b) Calcule a energia cinética total do sistema anel-mesa logo antes da colisão () e
logo depois que o anel e a mesa começam a girar com mesma velocidade angular ().
c) Calcule a energia dissipada pelo atrito entre a mesa e os rolamentos durante o intervalo
de tempo de 1,9 s a 2,4 s.
d)Calcule a energia dissipada pelo atrito entre a mesa e o anel durante o intervalo de
tempo de 1,9 s a 2,4 s.
Passo 1
a)
Nessa questão a gente tem que focar bem no gráfico para poder extrair a maior quantidade de dados possíveis. Como ele ta pedindo o torque , podemos usar duas relações, a que o gráfico nos der a gente usa.
Sabemos que o torque pode ser calculado por ou .
De fato ele não falou nada sobre forças, apenas que elas existiam, mas não quantificou nada. Em contrapartida ele nos deu o e no gráfico tem como achar o de boa, então é bem melhor usar a segunda relação.
Como? Simples!
Pelo gráfico a gente vê que na primeira descida esses valores serão:
E daí achamos o :
Passo 2
Agora é só substituir na fórmula do torque e pa-bum!
Passo 3
b)
Questão bem simples também, basta olhar no gráfico quais os dados que precisamos. Sabemos todos que a fórmula da energia cinética para rotação é:
Nosso poderá ser calculado com o certo?
Lá no gráfico a gente vê que o
Substituindo na fórmula e claro, deixando em função de já que ele não deu nenhum valor, vai ficar:
Já o a gente usa o , que vai ser . Só que dessa vez o momento de inércia vai ser o dobro, pois a peça agora vai estar acoplada, ambas com a mesma velocidade. Usando a fórmula, teremos:
Passo 4
c)
Sabemos que o trabalho na rotação pode ser calculada por:
“Abrindo” mais as contas, a gente vai ter:
Lá da cinemática de rotação a gente já viu que...
Tacando isso na fórmula do trabalho, vamos ter:
Passo 5
Como já calculamos lá no Passo 1, o será:
Como nosso , e como a gente viu na letra a.
Substituindo tudo, teremos:
Passo 6
d)
Já que a gente já sabe quanto vale o , podemos achar o .Toda a energia dissipada entre entre e será o ocasionado pelo atrito, seja entre a mesa e o anel e a mesa e o rolamento. Dessa forma podemos fazer:
Mas lááá do Teorema do Trabalho-Variação Energia Cinética, a gente pode tirar a relação:
O nosso por sua vez, será a diferença entre a energia cinética final e inicial, escrita por:
Assim, o será...
Looooogo:
Resposta
- ;