Um bloco de inércia sobre uma rampa sem atrito está preso a um barbante fino. O barbante passa por uma polia e está preso a uma massa pendurada . A rampa está inclinada com um ângulo de acima da horizontal.
- Considerando a polia ideal e sem atrito, determine o valor de que faz o sistema se mover de forma que o bloco de inércia suba a rampa com velocidade constante.
- Considerando agora que a polia é um disco com inércia e raio , determine o valor de que faz o sistema se mover e forma que o bloco de inércia suba a rampa com aceleração .
Passo 1
Fala galera, tudo bem? A primeira coisa que vou falar dessa questão é que a rampa é sem atrito! Então podemos esquecer (só um pouquinho hihihi) eu existe a força de atrito, ok?
No item (a) o problema quer saber o valor da massa , aquela está pendurada, que faz o sistema se mover de forma que o bloco de inércia suba a rampa com velocidade constante. A expressão chave aqui é velocidade constante. Se o sistema todo vai estar com velocidade constante, isso significa que não haverá força resultante no sistema!
Beleza?
Passo 2
Já sabemos, de outros carnavais, que a força que puxa o bloco que está na rampa pra baixo é a componente horizontal do peso e ele está relacionado com a inclinação da rampa:
E essa força será igual à tensão no fio!
Já para o bloco pendurado, temos apenas a força peso agindo, então temos:
E é igual em módulo à tensão na corda:
Como a corda é a mesma nesse sistema, então podemos usar essas duas expressões e eliminar a tensão:
E simplificando temos:
Pronto! Como o problema não nos deu os valores das massas e nem da inclinação, a resposta fica essa aí mesmo! =D
Vamos resolver o item (b)?
Passo 3
No item (b) o problema nos diz que a polia é um disco, sendo assim temos que relembrar da fórmula do momento de inércia de um disco:
E agora as tensões não serão mais iguais, mas calma! Vamos ter outras equações para eliminar essas tensões das nossas vidas =P
Agora precisamos equacionar não só os blocos, como também a polia! Devemos lembrar também que agora o sistema não está mais em equilíbrio, mas sim com uma aceleração positiva (para o bloco ) de valor . Vamos começar pelos blocos que a gente já estava acostumada. Vou fazer um diagrama de corpo livre pra gente entender melhor:
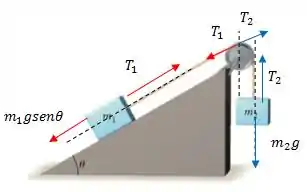
No bloco sobre a rampa temos duas forças: tensão e puxando pra baixo a componente horizontal do peso . E essas duas forças devem ser capaz de fazer com que esse bloco suba a rampa com uma aceleração de , então vamos equacionar isso. Usando a segunda lei de Newton temos:
Agora vou fazer isso também para o bloco que está pendurado. Saca só: nele estão agindo a tensão e o peso também, e como o sistema está se movimentando todo em conjunto, a aceleração dele também é (mas agora o sentido positivo é pra baixo), assim aplicando de novo a lei de Newton temos:
Agora vou somar essas duas equações, deixando as tensões de um lado e as massas e outros fatores do outro:
Passo 4
Ta, e agora? Calma! Temos ainda que olhar pra polia com mais carinho! Ela tem momento de inércia, não tem? Então ela contribui também para o movimento! A tensão gera um torque positivo nela, enquanto que a tensão , negativo. Essa diferença de torques aplicados nela gera uma aceleração angular , que podemos escrever em termos da aceleração linear () e do raio da polia!
Lembra que o torque é o produto da força pelo braço de alavanca! Nesse caso, a força é a tensão e o braço de alavanca é o próprio raio da polia =)
Assim, aplicando a segunda lei de Newton para as rotações na polia temos:
Olha só que legal! Agora temos uma expressão para a diferença de tensões! Exatamente o que não sabíamos na expressão ali em cima!
Agora é só substituir:
Aqui só cuida o sinal tá!
Podemos cancelar em todos os fatores e é só trabalho braçal:
Ufa! Acabou! Tranquilo? Toma um suco e borá pra próxima questão!
=D