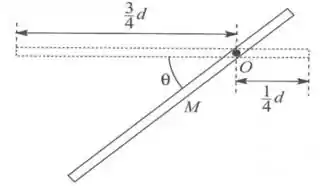
Uma haste metálica fina e homogênea, de comprimento e massa , pode girar livremente em torno de um eixo horizontal que a atravessa perpendicularmente em um ponto O distante de uma suas das extremidades, conforme mostrado na figura. A haste é solta a partir do repouso de uma posição horizontal, portanto, estando com sua dimensão maior paralela ao chão.

1. Calcule o momento de inércia da haste com respeito ao eixo em torno do qual ela gira.
2. Calcule a velocidade angular adquirida pela haste após ela ter caído de um ângulo , conforme indicado na figura.
3. Calcule a aceleração da haste após ela ter caído do mesmo ângulo

Dado: Momento de inércia de uma barra de massa e comprimento cujo eixo de rotação passa pelo seu centro de massa:

Bom galera, a gente vai ter que usar a relação entre torque, momento angular e velocidade angular.

A relação não vetorial é assim:

E:

Bom, mas o torque que age sobre a barra é o torque da força peso. Para descobrir o torque temos que pegar a componente do peso que é perpendicular à barra

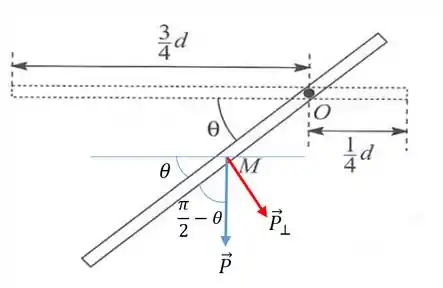
Seu módulo é dado por:

Onde

Então:

Fazendo a expansão do seno

Assim finalmente

Beleza? Mas como você pode ver esse torque varia de acordo com o ângulo

Então teremos que integrar essa parada.

De acordo com a equação:

Vamos integrar e assim descobrir a variação de momento angular. No entanto, como a barra parte do repouso, o momento inicial é nulo:

Logo:

Então:

Lembrando que o ângulo inicial é

Assim:

Então:

Mas como:

Então:

c):

Bom, aqui só a gente usar a formula:

Precisamos usar o valor do torque quando ele atinge o ângulo

Então: