Um disco está livre para girar em torno de um eixo fixo que passa pelo . Uma força de módulo conhecido, , deve ser aplicada no plano do disco. Entre as opções abaixo, a aceleração angular será maior se a força for aplicada:
- Tangencialmente, em um ponto a meio caminho entre o eixo e a borda.
- Radialmente, em um ponto a meio caminho entre o eixo e a borda.
- Radialmente, em um ponto da borda.
- Em um ponto da borda, mas nem radialmente nem tangencialmente.
- Tangencialmente, em um ponto da borda.
Passo 1
Bom galera, de acordo com a equação abaixo:
Quanto maior o módulo do torque, maior o módulo da aceleração angular.
Mas como o torque também é dado por:
Onde vai ser o ângulo entre o braço e a força . Assim:
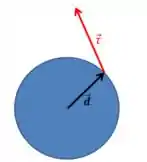
Assim, a melhor forma de aumentar o módulo desse torque é aumentando o módulo do braço e maximizando aquele seno ali.
Passo 2
A melhor forma de se fazer isso é fazendo:
E:
Em outras palavras, aplicando a força na borda do disco, de modo que ela faça um ângulo de com a direção radial, ou seja, que ela seja tangente à borda:
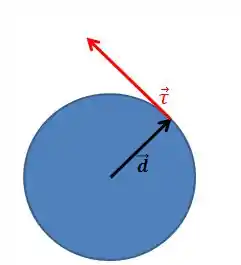
Assim:
e)
Resposta
e)