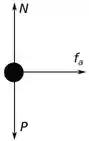
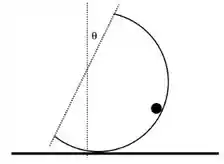
Q - Considere uma bola de massa fixa em uma semi-circunferência rígida de raio e de massa muito menor que a massa da bola. Inicialmente o dispositivo é abandonado de acordo com a figura, onde , e rola sem deslizar sobre a superfície horizontal.

Desenhe o diagrama de corpo livre do sistema bola semi-circunferência, e escreva as equações de movimento do sistema (não precisa resolvê-las).

Desenhe o diagrama de corpo livre estendido, e complemente as equações do item anterior com a equação para rotações (não precisa resolvê-las).

Primeiro vamos ver o item .

No sistema massa semi-circunferência, temos apenas a força peso que age no sistema que aponta para baixo, a força de atrito que faz com que o sistema gire sem deslizar e aponta para a direita e por último a normal que aponta para cima.

Então o diagrama fica da seguinte forma:

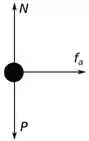
E agora as equações de movimento teremos uma na direção e outra na direção . Na direção temos apenas a força de atrito e na direção temos a força peso e a força normal, assim:

Agora vamos atrás do diagrama de corpo livre estendido. Esse diagrama seria de cada corpo do sistema, mas como só a massa que está fixa tem massa não desprezível, então basta fazer o diagrama dela.

Vamos fazer o digrama com ela na posição mostrada na figura do enunciado.

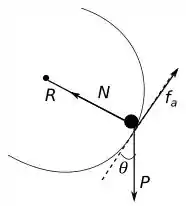
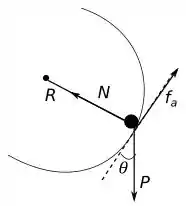
Agora a equação de movimento para rotação se dar que o torque resultante é igual a soma dos torques realizados pelas forças que agem na massa .

Olhando o diagrama podemos ver que as únicas forças que causam torque na massa é a força de atrito e a componente de que é perpendicular a reta que liga o centro e a massa.

A força de atrito causa um torque negativo, e a componente da força peso realiza um torque positivo. Assim: