Um pêndulo simples é formado por uma partícula de massa ligada a uma corda de comprimento de massa desprezível. Ele está preso num ponto de suspensão O, inicialmente em sua posição vertical e é deslocado de um ângulo , de onde passa a executar um movimento oscilatório. Podemos afirmar que:
a) O vetor aceleração do sistema é constante, uma vez que as forças atuantes possuem módulo constantes.
b) O torque produzido pela força peso calculado a partir do ponto O no instante em que a partícula atinge a posição angular é dado por e é perpendicular ao plano de oscilação do pêndulo.
c) Adotando como referência a posição vertical da partícula (q = 0), sua energia potencial máxima é dada por ).
d) O movimento da partícula possui momento angular constante e perpendicular ao plano da folha.
e) Todas as alternativas acima estão corretas.
Passo 1
Bora ver a letra A:
Para que o vetor aceleração permaneça constante, temos que olhar para o vetor da força resultante , pois um é consequência do outro:
Vamos dar uma olhada no módulo da força resultante em cada eixo...
Isolando as forças, teremos:
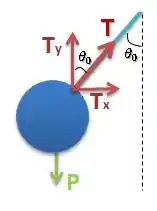
Para o eixo , temos:
Já para o eixo :
Dessa forma, podemos ver que a aceleração depende de , ou seja, como varia, a aceleração não será constante.
Passo 2
Letra B:
O Torque de uma força é calculado por:
Nesse caso, o vetor é o vetor posição que parte do ponto de suspensão O e vai até o ponto de aplicação da força peso :
Um produto vetorial entre dois vetores sempre resulta em um terceiro vetor perpendicular aos outros dois.
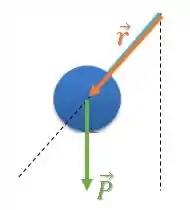
Como os vetores e sempre estão no plano de oscilação do pêndulo, o vetor torque estará sempre perpendicular a esse plano.
Então, essa parte da afirmativa confere...
Vamos dar uma olhada agora no módulo do torque , que é dado por:
Onde é o ângulo entre os vetores.
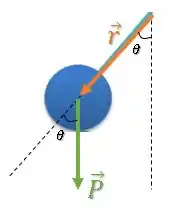
Pela figura, vemos que o ângulo entre os vetores é o mesmo ângulo de inclinação do pêndulo (ângulo ), então o torque é:
Substituindo por e o módulo do vetor posição pelo comprimento do fio , temos:
Ou seja:
Ta certinho!
OBS: Se você pensou em usar esse ângulo aqui () como o ângulo entre os dois vetores:
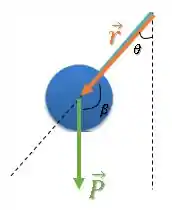
Também estaria certo, pois o ângulo e o ângulo apresentam o mesmo :
Isso porque esses dois ângulos somam .
Então, o torque ficaria a mesma coisa:
Porém, você precisaria perceber esse detalhe para saber que a letra B é a resposta correta.
Resposta
Letra B