Um parafuso deve ser apertado com um torque de no sentido horário, aplicando-se uma das forças mostradas na chave da figura. As intensidades das forças são e . Qual das forças abaixo produz o torque necessário?
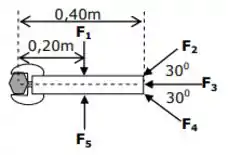
(A)
(B)
(C)
(D)
(E)
Passo 1
O enunciado diz que o torque sobre o parafuso deve:
- ser no sentido horário
- ter um módulo de
Queremos saber qual dessas forças consegue gerar esse torque desejado.
Passo 2
Vamos olhar para a primeira condição.
Se o torque sobre o parafuso é no sentido horário, a força deve tentar fazer a chave de fenda (ferramenta presa à porca) girar no sentido horário.
A força não tenta girar essa chave de fenda em nenhum dos sentidos:
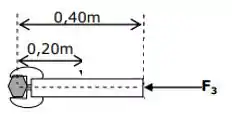
Isso porque ela está aplicada na direção passando pelo centro de rotação (porca), então seu torque é nulo.
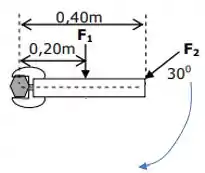
As forças e tentam girar a chave de fenda no sentido anti-horário:
Assim, não servem para gerar o torque que queremos.
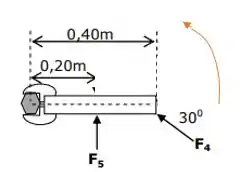
Já as forças e tentam girar a chave de fenda no sentido horário:
Então, ficamos entre essas duas forças.
Passo 3
Agora que já sabemos quais duas forças geram torque no sentido horário, vamos calcular o módulo do torque (valor sem se preocupar com sinal ou direção).
Torque de :
Será o produto vetorial entre o vetor posição (liga a porca ao ponto de aplicação da força) com o vetor da força :
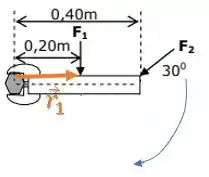
O módulo desse produto vetorial será:
Sendo o ângulo entre os vetores.
Como os vetores são perpendiculares, temos:
Substituindo os valores:
Opa, então a força não gera o módulo do torque que queremos.
Torque de :
Será o produto vetorial entre o vetor posição (liga a porca ao ponto de aplicação da força) com o vetor da força :
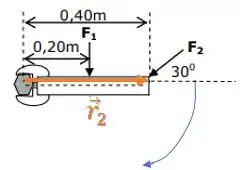
O módulo desse produto vetorial será:
Mas agora, o ângulo vale :
Assim, achamos que a força gera um torque na porca de valor no sentido horário.
Resposta
Letra (B)